题目内容
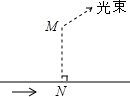 一辆小车沿着水平地面上的长直轨道匀速的向右运动,有一台散发出细光束的激光器装在小转台M上,转台到轨道的距离MN=10米.转台匀速的转动,使激光器在水平面内扫描.扫描一周的时间为60秒,光束转动的方向为逆时针方向.已知当光束与MN的夹角为45°时,光束正好射到小车上,如果再经过2.5秒,光束又射到小车上,求小车的速度?(
一辆小车沿着水平地面上的长直轨道匀速的向右运动,有一台散发出细光束的激光器装在小转台M上,转台到轨道的距离MN=10米.转台匀速的转动,使激光器在水平面内扫描.扫描一周的时间为60秒,光束转动的方向为逆时针方向.已知当光束与MN的夹角为45°时,光束正好射到小车上,如果再经过2.5秒,光束又射到小车上,求小车的速度?(| 3 |
考点:解直角三角形的应用
专题:
分析:首先正确做出图形,再根据当光束与MN的夹角为45°时,光束正好射到小车上,根据题意求出经过△t=2.5(s)光束转过的角度,2.5s后光束又射到小车上,根据题意做出光路图,由图求出小车在这段时间内的路程,然后利用速度公式计算出小车的速度即可.
解答:解:①作图
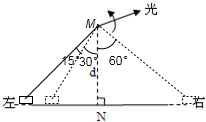
②△t时间内光束转过的角度△θ=
×360°=15°;
有两种可能:
(1)光束射到小车上,小车正在接近N点,△t时间内光束与MN之夹角从45°变为30°,v1≈1.69m/s;
(2)光束射到小车上,小车正在远离N点,△t时间内光束与MN之夹角从45°变为60°,v2≈2.92m/s;
答:若小车正在接近N点,则小车的速度约为1.69m/s;
若小车正在远离N点,则小车的速度约为2.92m/s.

②△t时间内光束转过的角度△θ=
| △t |
| t |
有两种可能:
(1)光束射到小车上,小车正在接近N点,△t时间内光束与MN之夹角从45°变为30°,v1≈1.69m/s;
(2)光束射到小车上,小车正在远离N点,△t时间内光束与MN之夹角从45°变为60°,v2≈2.92m/s;
答:若小车正在接近N点,则小车的速度约为1.69m/s;
若小车正在远离N点,则小车的速度约为2.92m/s.
点评:本题考查了解直角三角形以及速度的计算,要熟记速度的计算公式,根据题意做出图,由图结合数学知识求出小车的路程是解题的关键.

练习册系列答案
相关题目
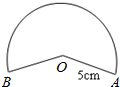 小明用图中的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,面积是15πcm2,那么这个的圆锥底面半径是( )
小明用图中的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,面积是15πcm2,那么这个的圆锥底面半径是( )| A、2cm | B、3cm |
| C、4cm | D、5cm |
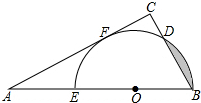 如图,把一块三角板(∠A=30°,∠C=90°,AC=6
如图,把一块三角板(∠A=30°,∠C=90°,AC=6 如图,长方形ABCD中,折痕为EF,将此长方形沿EF折叠,使点B与点D重合,已知AB=3cm,AD=9cm.求EF的长.
如图,长方形ABCD中,折痕为EF,将此长方形沿EF折叠,使点B与点D重合,已知AB=3cm,AD=9cm.求EF的长.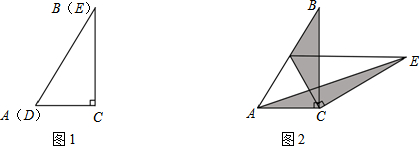
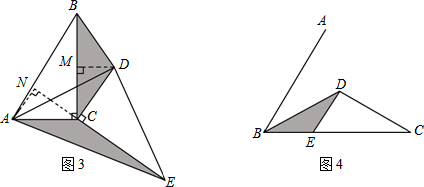
 如图,P、Q分别是正方形ABCD的边AB、BC上的点,且BP=BQ,过B点作PC的垂线,垂足为H.
如图,P、Q分别是正方形ABCD的边AB、BC上的点,且BP=BQ,过B点作PC的垂线,垂足为H.