Question

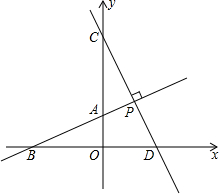如图，直线AB与坐标轴分别交于点A、点B，且OA、OB的长分别为方程x²-6x+8=0的两个根（OA＜OB），点C在y轴上，且OA：AC=1：2，D（3，0）直线CD垂直于直线AB于点P，交x轴于点D．
（1）求出点A、点B的坐标．
（2）请求出直线CD的解析式．
（3）若点M为坐标平面内任意一点，在直线AB上是否存在这样的点M，使以点B、D、M为顶点的三角形与△AOB相似？若存在，请直接写出点M的坐标；若不存在，请说明理由．

Answer 1

考点：一次函数综合题

专题：

分析：（1）根据一元二次方程的解法得出0A=2，0B=4，即可得出的A，B的坐标；
（2）设直线CD的解析式为y=kx+b，把点C、D的坐标代入函数关系式，利用待定系数法求一次函数解析式；
（3）需要分类讨论：△DMB∽△AOB和△MDB∽△AOB两种情况，利用相似三角形的对应边成比例来求点M的坐标．

解答： 解：（1）∵x²-6x+8=0，
∴x₁=4，x₂=2                            
∵0A、0B为方程的两个根，且0A＜0B，
∴0A=2，0B=4                         
∴A（0，2），B（-4，0）；

（2）∵0A：AC=1：2，OA=2，
∴AC=4，
∴OC=OA+AC=2+4=6，
∴C（0，6），
设直线CD的解析式为y=kx+b（k≠0），
把C（0，6），D（3，0）分别代入得：

6=b 3k+b=0

解得

k=-2 b=6

，
∴直线CD的解析式为：y=-2x+6；

（3）存在，理由如下：
由A（0，2），B（-4，0）得到直线AB的解析式为：y=

1

2

x+2．
设M（x，y）．
当△MDB∽△AOB时，∠BDM=∠BOA=90°，且

BD

BO

=

DM

OA

，即

7

4

=

y

2

，
解得 y=

7

2

．
则

7

2

=

1

2

x+2，
解得 x=3．
即M（3，

7

2

）；
同理，当△DMB∽△AOB时，M（

8

5

，

14

5

）．
综上所述，符合条件的点M的坐标是（3，

7

2

）或（

8

5

，

14

5

）．

点评：此题主要考查了待定系数法求一次函数解析式以及相似三角形的判定和一元二次方程的解法等知识，相似三角形与函数经常综合出现，同学们应注意灵活应用．