题目内容
如图①所示是一个长为2m,宽2n的长方形,沿图中虚线用剪刀均分成四个长方形,然后按图②的方式拼成一个正方形
(1)你认为图②中的阴影部分的正方形的边长等于 ;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.方法① 方法②
(3)仔细观察,写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系;
(4)根据(3)题中的等量关系,解决如下问题:a+b=3,ab=1,求(a-b)2的值.

(1)你认为图②中的阴影部分的正方形的边长等于
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.方法①
(3)仔细观察,写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系;
(4)根据(3)题中的等量关系,解决如下问题:a+b=3,ab=1,求(a-b)2的值.

考点:列代数式,代数式求值
专题:
分析:平均分成后,每个小长方形的长为m,宽为n.
(1)正方形的边长=小长方形的长-宽;
(2)第一种方法为:大正方形面积-4个小长方形面积,第二种表示方法为:阴影部分为小正方形的面积;
(3)利用(m+n)2-4mn=(m-n)2可求解;
(4)利用(a-b)2=(a+b)2-4ab可求解.
(1)正方形的边长=小长方形的长-宽;
(2)第一种方法为:大正方形面积-4个小长方形面积,第二种表示方法为:阴影部分为小正方形的面积;
(3)利用(m+n)2-4mn=(m-n)2可求解;
(4)利用(a-b)2=(a+b)2-4ab可求解.
解答:
解:(1)阴影部分的正方形的边长等于m-n;
(2)方法①(m+n)2-4mn;②(m-n)2;
(3)(m+n)2-4mn=(m-n)2;
(4)∵a+b=3,ab=1,
∴(a-b)2=(a+b)2-4ab=9-4=5.
(2)方法①(m+n)2-4mn;②(m-n)2;
(3)(m+n)2-4mn=(m-n)2;
(4)∵a+b=3,ab=1,
∴(a-b)2=(a+b)2-4ab=9-4=5.
点评:本题考查了列代数式的知识,解决问题的关键是读懂题意,找到所求的量的等量关系.本题更需注意要根据所找到的规律做题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列运算正确的是( )
| A、(a3)2=a9 |
| B、(3x)2=3x2 |
| C、x3•x=x4 |
| D、(x+1)2=x2+1 |
下列说法正确的有( )
| A、4的平方根是2 |
| B、-8没有立方根 |
| C、8的立方根是±2 |
| D、9的算术平方根是3 |
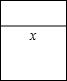 用18米长的铝合金做成一个长方形的窗框(如图),设长方形窗框的横条长度为x米,则长方形窗框的面积为( )
用18米长的铝合金做成一个长方形的窗框(如图),设长方形窗框的横条长度为x米,则长方形窗框的面积为( )| A、x(18-x)平方米 | ||
| B、x(9-x)平方米 | ||
C、x(
| ||
D、x(
|
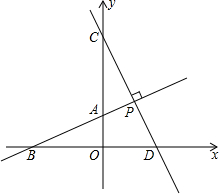 如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA:AC=1:2,D(3,0)直线CD垂直于直线AB于点P,交x轴于点D.
如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA:AC=1:2,D(3,0)直线CD垂直于直线AB于点P,交x轴于点D.