题目内容
已知代数式2mx2-3x+4y-1与x2+nx+y的和与字母x的取值无关，其中m、n是常数，那么mn= ．
考点：整式的加减
专题：
分析：根据题意可得，x2和x的系数均为0，据此求出m、n的值，然后求解mn．
解答：
解：2mx2-3x+4y-1+x2+nx+y=（2m+1）x2+（n-3）x+5y-1，
∵代数式之和与字母x的取值无关，
∴2m+1=0，n-3=0，
∴m=-
，n=3，
则mn=（-
）3=-
．
故答案为：-
．
∵代数式之和与字母x的取值无关，
∴2m+1=0，n-3=0，
∴m=-
| 1 |
| 2 |
则mn=（-
| 1 |
| 2 |
| 1 |
| 8 |
故答案为：-
| 1 |
| 8 |
点评：本题考查了整式的加减，解答本题的关键是掌握去括号法则和合并同类项法则．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
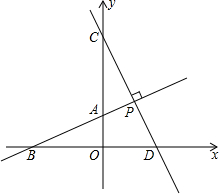如图，直线AB与坐标轴分别交于点A、点B，且OA、OB的长分别为方程x2-6x+8=0的两个根（OA＜OB），点C在y轴上，且OA：AC=1：2，D（3，0）直线CD垂直于直线AB于点P，交x轴于点D．下列说法中不正确的是（ ）
| A、最小的正整数是1 |
| B、最大的负整数是-1 |
| C、有理数分为正数和负数 |
| D、绝对值最小的有理数是0 |
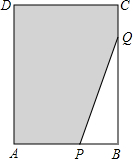如图，在长方形ABCD中，AB=6，CB=8，点P与点Q分别是AB，CB边上的动点，点P与点Q同时出发，点P以每秒2个单位长度的速度从点A→点B运动，点Q以每秒1个单位长度的速度从点C→点B运动．当其中一个点到达终点时，另一个点也随之停止运动．设运动时间为t秒，阴影部分的面积为Sm2．