Question

7．定义：如果三角形有一边上的中线恰好等于这边的长，那么称这个三角形为“匀称三角形”．若Rt△ABC为匀称三角形，且∠C=90°，AC=4，则BC=$\frac{8\sqrt{3}}{3}$或2$\sqrt{3}$．

Answer 1

分析 根据题意分三种情况进行讨论，画出相应的图形，即可求得BC边的长．

解答 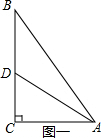解：如右图一所示，
若AD是BC边上的中线，则BC=AD，
设AD=BC=2x，
则CD=x，
∴$\sqrt{{x}^{2}+{4}^{2}}=2x$，得x=$\frac{4\sqrt{3}}{3}$，
∴2x=$\frac{8\sqrt{3}}{3}$，
即BC=$\frac{8\sqrt{3}}{3}$；
如右图二所示，
若BE是边AC上的中线，则AC=BE，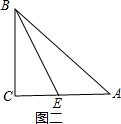
∴BE=4，CE=2，
∴BC=$\sqrt{B{E}^{2}-C{E}^{2}}=2\sqrt{3}$；
∵AB边上的中线是AB边的一半，故AB边上的中线等于AB的长这种情况不存在；
故答案为：$\frac{8\sqrt{3}}{3}$或2$\sqrt{3}$．

点评 本题考查勾股定理，解题的关键是明确题意，画出相应的图形，利用分类讨论的数学思想解答问题．