题目内容
17.吴老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.
(1)如图(1)正方体的棱长为5cm,一只蚂蚁欲从正方体底面上的点A沿正方体表面爬到点C1处;
(2)如图(2)长方体底面是边长为5cm的正方形,高为6cm,一只蚂蚁欲从长方体底面上的点A沿长方体表面爬到点C1处;
(3)如图(3)是底面周长为10cm,高为5cm的圆柱体,一只蚂蚁欲从圆柱体底面上的点A沿圆柱体表面爬到点C处.
分析 (1)将正方体展开,连接AC1,即可求得最短路径的长;
(2)将长方体展开,得到两个结果,取其值最小者;
(3)根据题意,先将圆柱体展开,再根据两点之间线段最短进行解答,再与未展开前作出比较,从而得到答案.
解答 解:(1)如图,AC1=$\sqrt{A{C}^{2}+C{{C}_{1}}^{2}}$=$\sqrt{(5+5)^{2}+{5}^{2}}$=5$\sqrt{5}$.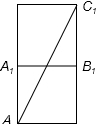
(2)分两种情况:
①如图,AC1=$\sqrt{(5+5)^{2}+{6}^{2}}$=2$\sqrt{34}$;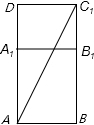
②如图,AC1=$\sqrt{(6+5)^{2}+{5}^{2}}$=$\sqrt{146}$.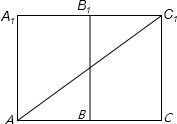 ,
,
因为$\sqrt{146}$>2$\sqrt{34}$,
所以最短路程为2$\sqrt{34}$cm.
(3)若展开圆柱体,BC为周长的一半,如图所示: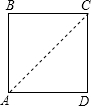
∵底面周长为10cm,
∴AD=5cm,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$cm.
可见最短路程的长为5$\sqrt{2}$.
点评 此题考查了平面展开---最短路径问题,将图形展开构造直角三角形求出斜边长是解题的关键.(3)中将圆柱体展开,根据两点之间线段最短,运用勾股定理解答即可.

练习册系列答案
相关题目
3.下列运算正确的是( )
| A. | $\sqrt{(-3)^{2}}$=-3 | B. | a2•a4=a6 | C. | (2a2)3=2a6 | D. | (a+2)2=a2+4 |
7.二次函数y=(x-1)(x-2)-1与x轴的交点x1,x2,x1<x2,则下列结论正确的是( )
| A. | x1<1<x2<2 | B. | x1<1<2<x2 | C. | x2<x1<1 | D. | 2<x1<x2 |
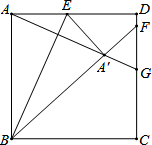 如图,点E为正方形ABCD边AD上的一点,且AE:DE=4:5,连接BE,将正方形沿着BE折叠,使A点落在A′点处,分别连接BA′、AA′交CD于点F、G.若FG=1,则正方形ABCD的边长为$\frac{72}{25}$.
如图,点E为正方形ABCD边AD上的一点,且AE:DE=4:5,连接BE,将正方形沿着BE折叠,使A点落在A′点处,分别连接BA′、AA′交CD于点F、G.若FG=1,则正方形ABCD的边长为$\frac{72}{25}$.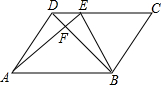 在平行四边形ABCD中,E是CD上一点,DE:EC=1:3,连AE,BE,BD且AE,BD交于F,则S△DEF:S△EBF:S△ABF=1:4:16.
在平行四边形ABCD中,E是CD上一点,DE:EC=1:3,连AE,BE,BD且AE,BD交于F,则S△DEF:S△EBF:S△ABF=1:4:16.