题目内容
9.将二次函数y=-2(x-1)2-1的图象先向右平移一个单位,再沿x轴翻折到x轴上方,然后向右平移一个单位,再沿y轴翻折到,再向右平移一个单位,再沿x轴翻折…以此类推,如果把向右平移一个单位再沿坐标轴翻折一次记作1次变换,那么二次函数y=-2(x-1)2-1的图象经过2015次变换后,得到的图象的函数解析式为y=-2(x+2)2-1.分析 先分别求出二次函数y=-2(x-1)2-1变换4次以后的函数解析式,发现规律:4次变换刚好又回到了原来的位置,那么变换2013次就相当于变换1次,即与变换1次的函数解析式相同.
解答 解:把y=-2(x-1)2-1的图象先向右平移一个单位,得y=-2(x-2)2-1,再沿x轴翻折到第一象限得-y=-2(x-2)2-1,即y=2(x-2)2+1,即1次变换后的解析式为y=2(x-2)2+1;
把y=2(x-2)2+1的图象先向右平移一个单位,得y=2(x-3)2+1,再沿y轴翻折到第二象限得y=2(-x-3)2+1,即y=2(x+3)2+1,即2次变换后的解析式为y=2(x+3)2+1;
把y=2(x+3)2+1的图象先向右平移一个单位,得y=2(x+2)2+1,再沿x轴翻折到第一象限得-y=2(x+2)2+1,即y=-2(x+2)2-1,即3次变换后的解析式为y=-2(x+2)2-1;
把y=-2(x+2)2-1的图象先向右平移一个单位,得y=-2(x+1)2-1,再沿y轴翻折到第二象限得y=-2(-x+1)2-1,即y=-2(x-1)2-1,即4次变换后的解析式为y=-2(x-1)2-1;
所以变换4次刚好又回到了原来的位置,
∵2015÷4=503…3,
∴变换2015次实际就相当变换3次,为y=-2(x+2)2-1.
故答案为y=-2(x+2)2-1.
点评 本题考查二次函数图象与几何变换,难度适中.根据解析式平移的规律:左加右减,上加下减分别求出二次函数y=-2(x-1)2-1变换4次以后的函数解析式,进而发现规律是解题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
4.根据表中二次函数y=ax2+bx+c的自变量x与函数值y的对应值,判断一元二次方程ax2+bx+c=0的一个根x的取值范围是( )
| x | 617 | 618 | 619 | 620 |
| y | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | 6<x<617 | B. | 617<x<618 | C. | 618<x<619 | D. | 619<x<7 |
14.已知y=ax2(a≠0)的图象不经过第四象限,图象上有A(-1,y1),B(-$\sqrt{2}$,y2),C(2,y3)三点,则y1、y2、y3的大小关系为( )
| A. | y1<y2<y3 | B. | y1>y2>y3 | C. | y2>y1>y3 | D. | y3>y1>y2 |
18.下列结论正确的是( )
| A. | $-\frac{3}{4}$的倒数是$\frac{4}{3}$ | B. | $-\frac{1}{3}$的相反数是$\frac{1}{3}$ | C. | -|-3|=3 | D. | 以上结论都不对 |
19.已知点A的坐标是(1,2),则点A关于x轴的对称点的坐标是( )
| A. | (1,-2) | B. | (-1,2) | C. | (-1,-2) | D. | (2,1) |

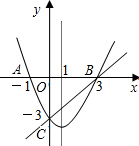 如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),一次函数的图象与抛物线交于B、C两点.
如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),一次函数的图象与抛物线交于B、C两点.