Question

14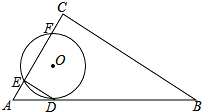．如图，⊙O与Rt△ABC的斜边AB相切于点D，与直角边AC相交于E、F两点，连结DE，已知∠B=30°，⊙O的半径为12，弧DE的长度为4π．
（1）求证：DE∥BC；
（2）若AF=CE，求线段BC的长度．

Answer 1

分析 （1）要证明DE∥BC，可证明∠EDA=∠B，由弧DE的长度为4π，可以求得∠DOE的度数，再根据切线的性质可求得∠EDA的度数，即可证明结论．
（2）根据90°的圆周角对的弦是直径，可以求得EF，的长度，借用勾股定理求得AE与CF的长度，即可得到答案．

解答 （1）证明：连接OD、OE，

∵AD是⊙O的切线，
∴OD⊥AB，∴∠ODA=90°，
又∵弧DE的长度为4π，
∴4π=$\frac{nπ×12}{180}$，
∴n=60，
∴△ODE是等边三角形，
∴∠ODE=60°，∴∠EDA=30°，
∴∠B=∠EDA，
∴DE∥BC．

（2）解：连接FD，

∵DE∥BC，
∴∠DEF=∠C=90°，
∴FD是⊙0的直径，
由（1）得：∠EFD=$\frac{1}{2}$∠EOD=30°，FD=24，
∴EF=12$\sqrt{3}$，
又∵∠EDA=30°，DE=12，
∴AE=4$\sqrt{3}$，
又∵AF=CE，∴AE=CF，
∴CA=AE+EF+CF=20$\sqrt{3}$，
又∵tan∠ABC=tan30°=$\frac{AC}{BC}$，
∴BC=60．

点评 本题考查了勾股定理以及圆的性质的综合应用，解答本题的关键在于90°的圆周角对的弦是直径这一性质的灵活运用．