题目内容
7.口袋里装有形状、大小完全相同的三个白球、两个红球,从中任意摸出两个球.(1)求摸出的两个球都是红球的概率;
(2)求摸出的两个球颜色相同的概率.
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与摸出的两个球都是红球的情况,再利用概率公式即可求得答案;
(2)由(1)中的树状图,可求得摸出的两个球颜色相同的情况,再利用概率公式即可求得答案.
解答 解:(1)画树状图得:
∵共有20种等可能的结果,摸出的两个球都是红球的有2种情况,
∴摸出的两个球都是红球的概率为:$\frac{2}{20}$=$\frac{1}{10}$;
(2)∵摸出的两个球颜色相同的有8种情况,
∴摸出的两个球颜色相同的概率为:$\frac{8}{20}$=$\frac{2}{5}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
17.已知二次函数y=a(x+3)2-h(a≠0)有最大值1,则该函数图象的顶点坐标为( )
| A. | (-3,-1) | B. | (-3,1) | C. | (3,1) | D. | (3,-1) |
19.下列命题中,逆命题错误的是( )
①如果两个三角形全等,那么这两个三角形的对应角相等.
②如果两个有理数相等,这两个数的平方也相等.
③若实数a、b 同为正数,则ab>0.
④在角的内部,与角的两边距离相等的点,一定在角平分线上.
①如果两个三角形全等,那么这两个三角形的对应角相等.
②如果两个有理数相等,这两个数的平方也相等.
③若实数a、b 同为正数,则ab>0.
④在角的内部,与角的两边距离相等的点,一定在角平分线上.
| A. | ①② | B. | ①②③ | C. | ③④ | D. | ①④ |
16.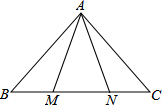 如图,∠B=50°,∠ANC=120°,AM=AN,则∠MAB的度数等于( )
如图,∠B=50°,∠ANC=120°,AM=AN,则∠MAB的度数等于( )
 如图,∠B=50°,∠ANC=120°,AM=AN,则∠MAB的度数等于( )
如图,∠B=50°,∠ANC=120°,AM=AN,则∠MAB的度数等于( )| A. | 10° | B. | 70° | C. | 60° | D. | 50° |