题目内容
5.5条直线两两相交,最多有10个交点.分析 5条直线两两相交,有5种位置关系,画出图形,进行解答.
解答 解:若5条直线两两相交,其位置关系有5种,如图所示:

则交点的个数有1个,或5个,或6个,或8个,或10个.
所以最多有10个交点,
故答案为:10
点评 本题主要考查了直线两两相交时交点的情况,关键是画出图形.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
16.在公式S=$\frac{1}{2}$(a+b)h中,已知a=3,b=4,h=-4,那么S=( )
| A. | -14 | B. | 14 | C. | 28 | D. | -28 |
13.某超市一月份的营业额为200万元,三月份的营业额为288万元,如果每月比上一个月增长的百分数相同,则每月的平均增长率为( )
| A. | 10% | B. | 15% | C. | 20% | D. | 25% |
10.在下列实数中,无理数是( )
| A. | 0.010010001 | B. | $\frac{1}{4}$ | C. | $\sqrt{5}$ | D. | 6 |
 在平面直角系中,已知A(-2,0),B(0,4),C(3,6);
在平面直角系中,已知A(-2,0),B(0,4),C(3,6);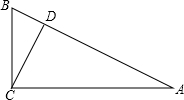 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.