题目内容
20.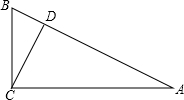 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.(1)请你写出图中有哪几对相似三角形;
(2)若BD=2,AD=8,请你选出最佳一对予以证明,并由此结论能直接求出CD的长.
分析 (1)利用两组角相等即可得到两个三角形相似可找到所有相似的三角形;
(2)利用(1)中的△ADC∽△CDB,可得到结论.
解答 解:(1)∵∠ACB=90°,CD⊥AB,
∴∠A+∠B=∠BCD+∠B,
∴∠A=∠BCD,且∠ADC=∠CDB,
∴△ADC∽△CDB,
在△ADC和△ACB中,∠A=∠A,∠ADC=∠ACB,
∴△ADC∽△ACB,
同理可得△CDB∽△ACB,
∴图中所有相似的三角形有:△ADC∽△CDB,△ADC∽△ACB,△CDB∽△ACB;
(2)由△ADC∽△CDB,可得$\frac{AD}{CD}=\frac{CD}{BD}$,
∴CD2=AD•DB,
∵BD=2,AD=8,
∴CD2=16,
∴CD=4.
点评 本题主要考查三角形相似的判定和性质,掌握相似三角形的判定方法是解题的关键,在该题的图形中注意利用同角的余角相等找到角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目