题目内容
5.设a2+2a-1=0,b4-2b2-1=0且1-ab2≠0.求代数式$\frac{a{b}^{2}+{b}^{2}+1}{a}$的值.分析 将两等式左右两边相减,左边整理后分解因式,根据1-ab2≠0的题设条件求得b2=-a,代入所求的分式化简,再将a2=-2a+1代入,整理后即可求出值.
解答 解:∵a2+2a-1=0,b4-2b2-1=0,
∴(a2+2a-1)-(b4-2b2-1)=0,
化简之后得到:(a+b2)(a-b2+2)=0,
若a-b2+2=0,即b2=a+2,则1-ab2=1-a(a+2)=1-a2-2a=0,与题设矛盾,所以a-b2+2≠0,
因此a+b2=0,即b2=-a,
又∵a2+2a-1=0,即a2=-2a+1,
∴$\frac{a{b}^{2}+{b}^{2}+1}{a}$=$\frac{-{a}^{2}-a+1}{a}$=$\frac{2a-1-a+1}{a}$=1.
点评 此题考查了根与系数的关系,一元二次方程ax2+bx+c=0(a≠0),当方程有解,即b2-4ac≥0时,设方程两根分别为x1,x2,则有x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
13.方程x2-2|x|+1=0的不同实数根的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
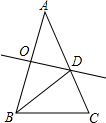 如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于O,交AC于D,连接BD.下列结论:①∠C=2∠A;②BD平分∠ABC;③S△BCD=S△BOD;④BC=BD,其中正确的结论有①②④.(只需填序号)
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于O,交AC于D,连接BD.下列结论:①∠C=2∠A;②BD平分∠ABC;③S△BCD=S△BOD;④BC=BD,其中正确的结论有①②④.(只需填序号)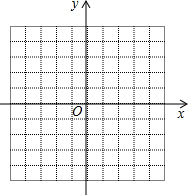 已知二次函数y=-$\frac{1}{2}$(x+4)2,将此函数的图象向右平移3个单位长度,再向上平移2个单位长度.
已知二次函数y=-$\frac{1}{2}$(x+4)2,将此函数的图象向右平移3个单位长度,再向上平移2个单位长度.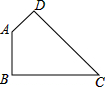 如图,在四边形ABCD中,∠BAD=135°,∠ABC=∠ADC=90°,DC=6,AD=2,求四边形ABCD的面积.
如图,在四边形ABCD中,∠BAD=135°,∠ABC=∠ADC=90°,DC=6,AD=2,求四边形ABCD的面积. 如图,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,则下列各式正确的是( )
如图,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,则下列各式正确的是( )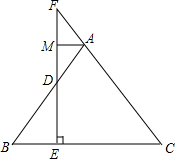 如图所示,在△ABC中,AB=AC,EF⊥BC于点E,点M是DF的中点,试说明AM⊥FD的理由.
如图所示,在△ABC中,AB=AC,EF⊥BC于点E,点M是DF的中点,试说明AM⊥FD的理由. 如图,直线y=kx+b过点C(1,3)与坐标轴分别交于点A(0,2)和点B.
如图,直线y=kx+b过点C(1,3)与坐标轴分别交于点A(0,2)和点B.