题目内容
9.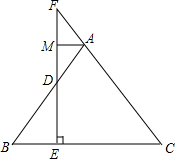 如图所示,在△ABC中,AB=AC,EF⊥BC于点E,点M是DF的中点,试说明AM⊥FD的理由.
如图所示,在△ABC中,AB=AC,EF⊥BC于点E,点M是DF的中点,试说明AM⊥FD的理由.
分析 根据AB=AC,得到∠B=∠C,由于EF⊥BC于点E,于是得到∠F+∠C=∠BDE+∠B=90°,等量代换得到∠F=∠ADF,求出AF=AD,根据等腰三角形的性质三线合一即可得到结论.
解答 解:∵AB=AC,
∴∠B=∠C,
∵EF⊥BC于点E,
∴∠F+∠C=∠BDE+∠B=90°,
∴∠F=∠BDE,
∵∠ADF=∠BDE,
∴∠F=∠ADF,
∴AF=AD,
∵点M是DF的中点,
∴AM⊥FD.
点评 本题考查了等腰三角形的判定和性质,直角三角形的性质,对顶角相等,熟练掌握各性质定理是解题的关键.

练习册系列答案
相关题目
14. 如图,△ABC≌△ADE,∠B=100°,∠BAC=40°,则∠AED=( )
如图,△ABC≌△ADE,∠B=100°,∠BAC=40°,则∠AED=( )
 如图,△ABC≌△ADE,∠B=100°,∠BAC=40°,则∠AED=( )
如图,△ABC≌△ADE,∠B=100°,∠BAC=40°,则∠AED=( )| A. | 70° | B. | 45° | C. | 40° | D. | 50° |
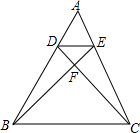 如图,在△ABC中,D、E分别是AB、AC上的点,DC交BE于F,且AD:AB=1:3,AE=$\frac{1}{2}$EC,求证:
如图,在△ABC中,D、E分别是AB、AC上的点,DC交BE于F,且AD:AB=1:3,AE=$\frac{1}{2}$EC,求证: 如图,若三角形内角和为180°且∠C+∠A=∠AEC,判断AB与CD是否平行,并说明理由.
如图,若三角形内角和为180°且∠C+∠A=∠AEC,判断AB与CD是否平行,并说明理由.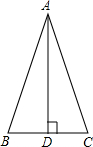 如图,AD是△ABC的高,若AB+BD=AC+CD,求证:△ABC是等腰三角形.
如图,AD是△ABC的高,若AB+BD=AC+CD,求证:△ABC是等腰三角形.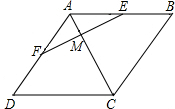 已知,如图,四边形ABCD是菱形,过AB的中点E作EF⊥AC于点M,交AD于点F,求证:AF=DF.
已知,如图,四边形ABCD是菱形,过AB的中点E作EF⊥AC于点M,交AD于点F,求证:AF=DF.