题目内容
分解因式：x4-2x3-2x2+2x+1．
考点：因式分解-分组分解法
专题：
分析：首先重新分组，进而利用十字相乘法以及公式法分解因式进而得出答案．
解答：解：x4-2x3-2x2+2x+1
=x4-2x3-3x2+x2+2x+1
=x2（x2-2x-3）+（x+1）2
=x2（x+1）（x-3）+（x+1）2
=（x+1）[x2（x-3）+x+1]
=（x+1）（x3-3x2+x+1）．
=x4-2x3-3x2+x2+2x+1
=x2（x2-2x-3）+（x+1）2
=x2（x+1）（x-3）+（x+1）2
=（x+1）[x2（x-3）+x+1]
=（x+1）（x3-3x2+x+1）．
点评：此题主要考查了分组分解法分解因式，正确应用公式法分解因式是解题关键．
练习册系列答案
名师点拨卷系列答案
相关题目
如图，在四边形PMNO中，MO⊥ON，各边的长度在图上已标出，求证：四边形PMON是平行四边形．
如图所示，矩形ABCD的对角线AC、BD相交于点O，BE平分∠ABC，交AC于点E，交CD于点F，且∠OBF=15°，求证：OF=EF．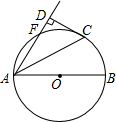
如图，AB是⊙O的直径，点F，C是⊙O上两点，且
