题目内容
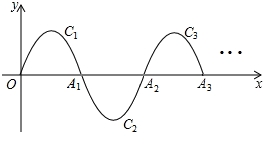
一段抛物线：y=﹣x（x﹣3）（0≤x≤3），记为C1，它与x轴交于点O，A1；将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3；…若P是其中某段抛物线上一点，则m=__________．
﹣2．
【考点】二次函数图象与几何变换．
【分析】求出抛物线C1与x轴的交点坐标，观察图形可知第偶数号抛物线都在x轴下方，再根据向右平移横坐标相加表示出抛物线C672的解析式，然后把点P的横坐标代入计算即可得解．
【解答】解：∵一段抛物线：y=﹣x（x﹣3）（0≤x≤3），
∴图象与x轴交点坐标为：（0，0），（3，0），
∵将C1绕点A1旋转180°得C2，交x轴于点A2；
将C2绕点A2旋转180°得C3，交x轴于点A3；
…
如此进行下去，直至得C10．
∴C672与x轴的交点横坐标为，，且图象在x轴下方，
∴C672的解析式为：y672=（x﹣2013）（x﹣2016），
当x=2015时，y=×=﹣2．
故答案为：﹣2．
【点评】本题考查了二次函数图象与几何变换，根据平移规律得出C672与x轴的交点坐标，进而得到解析式是解题关键．
练习册系列答案
相关题目
B．
C．
D．
的图象在第二、第四象限内，函数图象上有两点A（2
，y1）、B（5，y2），则y1与y2的大小关系是__________．
x+30（1≤x≤20，且x为整数），后10天的销售价格Q2（元/件）与销售时间x（天）之间有如下关系：Q2=45（21≤x≤30，且x为整数）．
=3﹣x，则x的取值范围是 ．