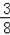题目内容
某大学毕业生响应国家“自主创业”的号召,投资开办了一个装饰品商店.该店采购进一种今年新上市的饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=﹣2x+80(1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:Q1=
 x+30(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
x+30(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
(1)试写出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)分别与销售时间x(天)之间的函数关系式;
(2)请问在这30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润.
注:销售利润=销售收入﹣购进成本.
【考点】二次函数的应用.
【专题】应用题;压轴题.
【分析】(1)运用营销问题中的基本等量关系:销售利润=日销售量×一件销售利润.一件销售利润=一件的销售价﹣一件的进价,建立函数关系式;
(2)分析函数关系式的类别及自变量取值范围求最大值;其中R1是二次函数,R2是一次函数.
【解答】解:(1)根据题意,得
R1=P(Q1﹣20)=(﹣2x+80)[(
 x+30)﹣20],
x+30)﹣20],
=﹣x2+20x+800(1≤x≤20,且x为整数),
R2=P(Q2﹣20)=(﹣2x+80)(45﹣20),
=﹣50x+2000(21≤x≤30,且x为整数);
(2)在1≤x≤20,且x为整数时,
∵R1=﹣(x﹣10)2+900,
∴当x=10时,R1的最大值为900,
在21≤x≤30,且x为整数时,
∵R2=﹣50x+2000,﹣50<0,R2随x的增大而减小,
∴当x=21时,R2的最大值为950,
∵950>900,
∴当x=21即在第21天时,日销售利润最大,最大值为950元.
【点评】本题需要反复读懂题意,根据营销问题中的基本等量关系建立函数关系式,根据时间段列出分段函数,再结合自变量取值范围分别求出两个函数的最大值,并进行比较,得出结论.

 名校课堂系列答案
名校课堂系列答案

 ﹣2 D.10﹣4
﹣2 D.10﹣4

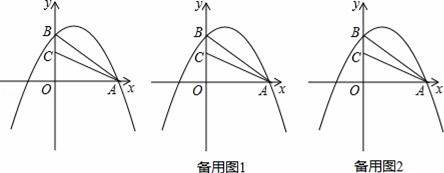
 x+3与x轴y轴分别交于点A、点B,抛物线y=﹣
x+3与x轴y轴分别交于点A、点B,抛物线y=﹣