题目内容
如图,在平四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)在直线AC的同侧,以点O为位似中心,作出△CON的位似三角形,并使△CON与和它位似的三角形的位似比是1:2.(写出结果,不写作法,保留作图痕迹).
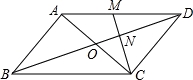
【考点】作图-位似变换;平行四边形的性质.
【分析】(1)根据平行四边形的性质得AD∥BC,AD=BC,OB=OD,则利用DM∥BC可判断△MND∽△CNB,所以MD:BC=DN:BN=1:2,设OB=OD=x,则BD=2x,BN=OB+ON=x+1,DN=x﹣1,于是得到x+1=2(x﹣1),解得x=3,所以BD=2x=6;
(2)如图,在OD上截取NG=ON,延长OC到H,使HC=OC,则△HOG满足条件.
【解答】解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OB=OD,
∴DM∥BC,
∴△MND∽△CNB,
∴MD:BC=DN:BN,
∵M为AD中点,
∴MD:BC=1:2,
∴DN:BN=1:2,即BN=2DN,
设OB=OD=x,则BD=2x,BN=OB+ON=x+1,DN=x﹣1,
∴x+1=2(x﹣1),解得x=3,
∴BD=2x=6;
(2)如图,△HOG为所作.

【点评】本题考查了作图﹣位似变换:先确定位似中心;②分别连接并延长位似中心和能代表原图的关键点;再根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了平行四边形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



 B.
B.


 ﹣2 D.10﹣4
﹣2 D.10﹣4