题目内容
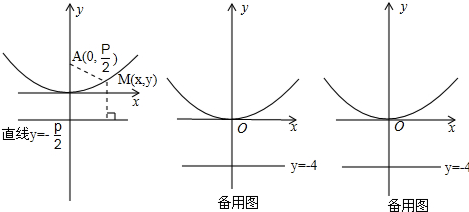
 如图,在平面直角坐标系中,直线y=-2x+42交x轴于点A,交直线y=x交于点B.抛物线y=ax2-2x+c分别交线段AB、OB于点C、D,点C和点D的横坐标分别为16和4.
如图,在平面直角坐标系中,直线y=-2x+42交x轴于点A,交直线y=x交于点B.抛物线y=ax2-2x+c分别交线段AB、OB于点C、D,点C和点D的横坐标分别为16和4.(1)求抛物线的解析式;
(2)若点Q为线段OB上一点,点P为抛物线上一点,且P、Q两点的纵坐标都为5,求线段PQ的长;
(3)若点Q为线段OB或线段BC上一点,点P为抛物线上一点,PQ⊥x轴.设P、Q两点之间的距离为d,点Q的横坐标为m,求m为何值时,d取得最大值,最大值是多少.并直接写出d随m的增大而减小时m的取值范围.
考点:二次函数综合题
专题:
分析:(1)易求得点C,D坐标,将C,D代入y=ax2-2x+c即可求得抛物线的解析式;
(2)根据纵坐标为5可以求得点P,Q的横坐标,即可求得PQ的长,即可解题;
(3)由题意知P、Q两点横坐标相同,分类讨论求得PQ的长,即可解题.
(2)根据纵坐标为5可以求得点P,Q的横坐标,即可求得PQ的长,即可解题;
(3)由题意知P、Q两点横坐标相同,分类讨论求得PQ的长,即可解题.
解答:解:(1)∵点C横坐标为16,且点C在直线y=-2x+42上,
∴点C坐标为(16,10),
∵点D横坐标为4,且点C在直线y=x上,
∴点D坐标为(4,4),
将C,D两点代入y=ax2-2x+c得:
,
解得:a=
,c=10,
∴抛物线的解析式为y=
x2-2x+10;
(2)抛物线上点P纵坐标为5,
则有5=
x2-2x+10,
解得:x=8±2
,
∴点P坐标(8+2
,5),(8-2
,5)
∵点Q为线段OB上一点,直线OB解析式为y=x,纵坐标为5,
∴点Q坐标为(5,5),
∴PQ长度为(8+2
-5)或(5-8+2
),即3+2
或2
-3;
(3)∵PQ⊥x轴,
∴P、Q两点横坐标相同,
∵直线y=-2x+42交直线y=x交于点B,
∴点B坐标为(14,14),
①当0≤m<4时,d=
m2-2m+10-m=
m2-3m+10,此时d有最大值m=0时,d=10,且此时d随m的增大而减小;
②当4≤m<14时,d=m-
m2+2m-10=-
m2+3m-10,此时d有最大值m=12时,d=8,∴m<12时,d随m的增大而增大,m≥12时,d随m的增大而减小;
③当14≤m<16时,d=-2m+42-(
m2-2m+10)=-
m2+32,此时d有最大值m=14时,d=7.5,且此时d随m的增大而减小;
综上所述,m=0时,d有最大值10,且d随m的增大而减小时m的取值范围为[0,4],[12,16].
∴点C坐标为(16,10),
∵点D横坐标为4,且点C在直线y=x上,
∴点D坐标为(4,4),
将C,D两点代入y=ax2-2x+c得:
|
解得:a=
| 1 |
| 8 |
∴抛物线的解析式为y=
| 1 |
| 8 |
(2)抛物线上点P纵坐标为5,
则有5=
| 1 |
| 8 |
解得:x=8±2
| 6 |
∴点P坐标(8+2
| 6 |
| 6 |
∵点Q为线段OB上一点,直线OB解析式为y=x,纵坐标为5,
∴点Q坐标为(5,5),
∴PQ长度为(8+2
| 6 |
| 6 |
| 6 |
| 6 |
(3)∵PQ⊥x轴,
∴P、Q两点横坐标相同,
∵直线y=-2x+42交直线y=x交于点B,
∴点B坐标为(14,14),
①当0≤m<4时,d=
| 1 |
| 8 |
| 1 |
| 8 |
②当4≤m<14时,d=m-
| 1 |
| 8 |
| 1 |
| 8 |
③当14≤m<16时,d=-2m+42-(
| 1 |
| 8 |
| 1 |
| 8 |
综上所述,m=0时,d有最大值10,且d随m的增大而减小时m的取值范围为[0,4],[12,16].
点评:本题是二次函数的综合题型,其中涉及到的知识点有二次函数解析式的确定、函数图象交点的求法等知识点.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
相关题目