题目内容
解方程:(2x-5)2-9(x+4)2=0.
考点:解一元二次方程-因式分解法
专题:计算题
分析:方程利用分解因式法求出解即可.
解答:解:分解因式得:(2x-5+3x+12)(2x-5-3x-12)=0,
即(5x+7)(-x-17)=0,
解得:x1=-
,x2=-17.
即(5x+7)(-x-17)=0,
解得:x1=-
| 7 |
| 5 |
点评:此题考查了解一元二次方程-因式分解法,熟练掌握因式分解法是解本题的关键.

练习册系列答案
相关题目
在平面直角坐标系中,函数y=x2-2x(x≥0)的图象为C1,C1关于原点对称的图象为C2,则直线y=a(a为常数)与C1、C2的交点共有3个,则a的取值范围是( )
| A、a<1 |
| B、-1<a<1 |
| C、-1≤a≤1 |
| D、a>1或a<-1 |
 如图所示,点D、E分别在AB、AC上,F为AB上一点,延长FE交BC的延长线于G,∠ECG=∠A+∠ADE,求证:DE∥BC.
如图所示,点D、E分别在AB、AC上,F为AB上一点,延长FE交BC的延长线于G,∠ECG=∠A+∠ADE,求证:DE∥BC.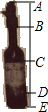 如图是一种盛装葡萄酒的瓶子,已知量得瓶塞AB与其下面部分BC的高度之比为2:3,C是BD的中点,且标签底部DE=
如图是一种盛装葡萄酒的瓶子,已知量得瓶塞AB与其下面部分BC的高度之比为2:3,C是BD的中点,且标签底部DE=