题目内容
11.(1)解方程:x2-3x-4=0(2)解不等式组:$\left\{\begin{array}{l}{2x-3≤x}\\{x+2<\frac{1}{2}x-1}\end{array}\right.$.
分析 (1)先因式分解,然后解方程;
(2)分别求出每个不等式的解集,再求出其公共部分.
解答 解:(1)方程可化为(x-4)(x+1)=0,
解得x1=4,x2=-1.
(2)由2x-3≤x可得x≤3,
由x+2<$\frac{1}{2}$x-1可得x<-6,
∴不等式组的解集为x<-6.
点评 (1)本题考查了解一元二次方程--因式分解法,熟悉十字相乘法是解题的关键;
(2)本题考查了解一元一次不等式组,熟悉不等式组的解法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.父子二人在周长为400m的环形跑道上练习跑步,同时同地背向起跑,20秒后两人第一次相遇,已知父速为子速的1.5倍.设儿子每秒跑xm,列方程为( )
| A. | 1.5x-x=1 | B. | 1.5x+x=1 | C. | 20(1.5x+x)=400 | D. | 20(1.5x-x)=400 |
19.在正三角形、平行四边、矩形和等腰梯形这四个图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 正三角形 | B. | 平行四边形 | C. | 矩形 | D. | 等腰梯形 |
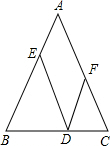 如图,在△ABC中,AB=AC,点D在BC上,DE∥AC交AB于点E,DF∥AB交AC于点F,试说明线段DE,DF,AB三者之间的数量关系.
如图,在△ABC中,AB=AC,点D在BC上,DE∥AC交AB于点E,DF∥AB交AC于点F,试说明线段DE,DF,AB三者之间的数量关系. 在△ABC中,∠BAC=∠BCA,CD平分∠ACB,CE⊥AB,交AB的延长线于点E,∠DCE=48°,求∠A的度数.
在△ABC中,∠BAC=∠BCA,CD平分∠ACB,CE⊥AB,交AB的延长线于点E,∠DCE=48°,求∠A的度数.