题目内容
1. 在△ABC中,∠BAC=∠BCA,CD平分∠ACB,CE⊥AB,交AB的延长线于点E,∠DCE=48°,求∠A的度数.
在△ABC中,∠BAC=∠BCA,CD平分∠ACB,CE⊥AB,交AB的延长线于点E,∠DCE=48°,求∠A的度数.
分析 根据角平分线的定义可得∠ACD=$\frac{1}{2}$∠BCA=$\frac{1}{2}$∠A,然后根据直角三角形两锐角互余列出方程求解即可.
解答 解:∵CD平分∠ACB,
∴∠ACD=$\frac{1}{2}$∠BCA=$\frac{1}{2}$∠A,
∵CE⊥AB,
∴∠A+∠ACD+∠DCE=90°,
∴∠A+$\frac{1}{2}$∠A+48°=90°,
解得∠A=28°.
点评 本题考查了三角形的内角和定理,角平分线的定义,利用∠A表示出∠ACD是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在-1,0,3和$\sqrt{2}$这四个实数中,负数是( )
| A. | -1 | B. | 0 | C. | 3 | D. | $\sqrt{2}$ |
 如图,∠A=31°,∠B=60°,∠BFD=52°,则∠C=37°.
如图,∠A=31°,∠B=60°,∠BFD=52°,则∠C=37°.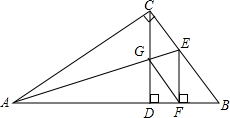 如图,AC⊥BC,AE平分∠CAB,CD⊥AB,EF⊥AB,连接FG,求证:CEFG为菱形.
如图,AC⊥BC,AE平分∠CAB,CD⊥AB,EF⊥AB,连接FG,求证:CEFG为菱形.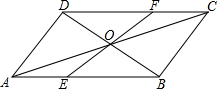 E,F分别是?ABCD的边AB,CD上的一点,且DF=BE,O是BD的中点,EF过点O.求证:EF与AC互相平分.
E,F分别是?ABCD的边AB,CD上的一点,且DF=BE,O是BD的中点,EF过点O.求证:EF与AC互相平分.