题目内容
8.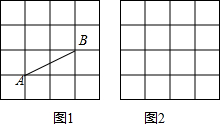 如图1,图2,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点.图1中的线段AB的两个端点都在格点上.
如图1,图2,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点.图1中的线段AB的两个端点都在格点上.(1)在图1中,线段AB的长为$\sqrt{5}$
(2)在图1中,画一个等腰直角三角形ABC,且三角形的顶点都在格点上;
(3)在图2中,画一个面积为10的正方形,且正方形的顶点都在格点上.
分析 (1)根据勾股定理进行计算即可得到AB的长;
(2)根据三角形ABC为等腰直角三角形,确定点C的位置,即可得到△ABC;
(3)根据正方形的面积为10,可得其边长为$\sqrt{10}$,据此可得正方形DEFG.
解答 解:(1)由勾股定理可得,AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
故答案为:$\sqrt{5}$;
(2)如图1所示,△ABC即为所求;
(3)如图2所示,四边形DEFG即为所求.
点评 本题主要考查了应用与设计作图以及勾股定理的运用,首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
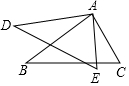 如图,请看以下两个推理过程:
如图,请看以下两个推理过程: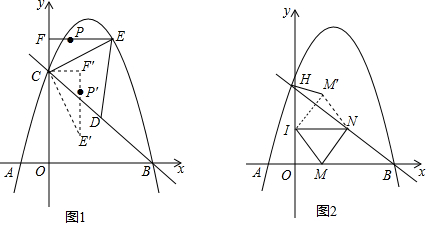
 将面积为$\sqrt{3}$cm2的等边三角形绕点O按顺时针方向依次旋转60°后得如图,则该图形的边长是2cm,图中共有6个平行四边形.
将面积为$\sqrt{3}$cm2的等边三角形绕点O按顺时针方向依次旋转60°后得如图,则该图形的边长是2cm,图中共有6个平行四边形.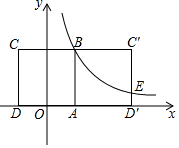 如图,边长为2的正方形ABCD关于y轴对称,边AD在x轴上,点B在第一象限,反比例函数y=$\frac{k}{x}$的图象经过点B,将正方形ABCD沿边AB翻折得到正方形ABC′D′,C′D′与y=$\frac{k}{x}$的图象交于点E.
如图,边长为2的正方形ABCD关于y轴对称,边AD在x轴上,点B在第一象限,反比例函数y=$\frac{k}{x}$的图象经过点B,将正方形ABCD沿边AB翻折得到正方形ABC′D′,C′D′与y=$\frac{k}{x}$的图象交于点E.