题目内容
5.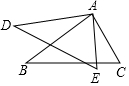 如图,请看以下两个推理过程:
如图,请看以下两个推理过程:①∵∠D=∠B,∠E=∠C,DE=BC,
∴△ADE≌△ABC(AAS);
②∵∠DAE=∠BAC,∠E=∠C,DE=BC,
∴△ADE≌△ABC(AAS).
则以下判断正确的(包括判定三角形全等的依据)是( )
| A. | ①对②错 | B. | ①错②对 | C. | ①②都对 | D. | ①②都错 |
分析 ①在△ADE和△ABC中,根据∠D=∠B、DE=BC、∠E=∠C利用全等三角形的判定定理(ASA)即可证出△ADE≌△ABC,①错误;②在△ADE和△ABC中,根据∠DAE=∠BAC、∠E=∠C、DE=BC利用全等三角形的判定定理(AAS)即可证出△ADE≌△ABC,②正确.综上即可得出结论.
解答 解:①在△ADE和△ABC中,$\left\{\begin{array}{l}{∠D=∠B}\\{DE=BC}\\{∠E=∠C}\end{array}\right.$,
∴△ADE≌△ABC(ASA),
∴①错误;
②在△ADE和△ABC中,$\left\{\begin{array}{l}{∠DAE=∠BAC}\\{∠E=∠C}\\{DE=BC}\end{array}\right.$,
∴△ADE≌△ABC(AAS),
∴②正确.
故选B.
点评 本题考查了全等三角形的判定,找出①利用全等三角形的判定定理(ASA)证出△ADE≌△ABC、②利用全等三角形的判定定理(AAS)证出△ADE≌△ABC是解题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
15.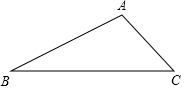 如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)
如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)
(1)用尺规作∠BAC的角平分线AE;
(2)用三角板作AC边上的高BD;
(3)用尺规作AC边上的垂直平分线MN.
 如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)
如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)(1)用尺规作∠BAC的角平分线AE;
(2)用三角板作AC边上的高BD;
(3)用尺规作AC边上的垂直平分线MN.
13. 如图,在4×4正方形网格中,黑色部分的 图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,黑色部分的 图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
 如图,在4×4正方形网格中,黑色部分的 图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,黑色部分的 图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )| A. | $\frac{3}{13}$ | B. | $\frac{4}{13}$ | C. | $\frac{5}{13}$ | D. | $\frac{6}{13}$ |
10.“每天锻炼一小时,健康生活一辈子”,自开展“阳光体育运动”以来,学校师生的锻炼意识都增强了.某校有学生8200人,为了解学生每天的锻炼时间,学校体育组随机调查了部分学生,统计结果如表所示.
表格中,m=30人; 这组数据的众数是14.5分钟;该校每天锻炼时间达到1小时的约有820人人.
表格中,m=30人; 这组数据的众数是14.5分钟;该校每天锻炼时间达到1小时的约有820人人.
| 时间段 | 频数 | 频率 |
| 29分钟及以下 | 108 | 0.54 |
| 30-39分钟 | 24 | 0.12 |
| 40-49分钟 | m | 0.15 |
| 50-59分钟 | 18 | 0.09 |
| 1小时及以上 | 20 | 0.1 |
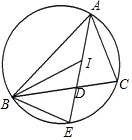 如图,点I是△ABC的内心,AI的延长线与边BC相交于点D,与△ABC的外接圆相交于点C.
如图,点I是△ABC的内心,AI的延长线与边BC相交于点D,与△ABC的外接圆相交于点C.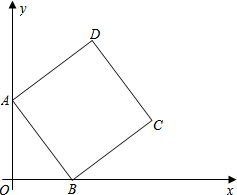 如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长满足(x-$\frac{7}{2}$)2=$\frac{1}{4}$中的x.其中OA>OB.
如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长满足(x-$\frac{7}{2}$)2=$\frac{1}{4}$中的x.其中OA>OB.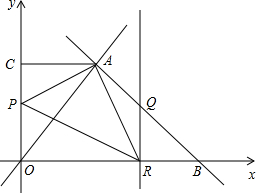 如图,已知直线y=-x+7与直线y=$\frac{4}{3}$x交于点A,且与x轴交于点B,过点A作AC⊥y轴与点C.点P从O点以每秒1个单位的速度沿折线O-C-A运动到A;点R从B点以相同的速度向O点运动,一个点到终点时,另一个点也随之停止运动.
如图,已知直线y=-x+7与直线y=$\frac{4}{3}$x交于点A,且与x轴交于点B,过点A作AC⊥y轴与点C.点P从O点以每秒1个单位的速度沿折线O-C-A运动到A;点R从B点以相同的速度向O点运动,一个点到终点时,另一个点也随之停止运动.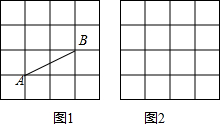 如图1,图2,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点.图1中的线段AB的两个端点都在格点上.
如图1,图2,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点.图1中的线段AB的两个端点都在格点上.