题目内容
18.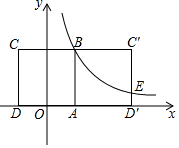 如图,边长为2的正方形ABCD关于y轴对称,边AD在x轴上,点B在第一象限,反比例函数y=$\frac{k}{x}$的图象经过点B,将正方形ABCD沿边AB翻折得到正方形ABC′D′,C′D′与y=$\frac{k}{x}$的图象交于点E.
如图,边长为2的正方形ABCD关于y轴对称,边AD在x轴上,点B在第一象限,反比例函数y=$\frac{k}{x}$的图象经过点B,将正方形ABCD沿边AB翻折得到正方形ABC′D′,C′D′与y=$\frac{k}{x}$的图象交于点E.(1)求反比例函数的解析式;
(2)求点E的坐标.
分析 (1)由正方形ABCD的边长为2且关于y轴对称得出点B的坐标,即可得出反比例函数解析式;
(2)由翻折性质得出点E的横坐标,结合解析式即可得其纵坐标.
解答 解:(1)∵四边形ABCD是正方形,
∴AB=BC=2,
∵正方形ABCD关于y轴对称,
∴OA=1,
∴点B的坐标为(1,2),
∴k=2,
∴反比例函数的解析式为y=$\frac{2}{x}$;
(2)∵正方形ABCD沿边AB翻折得到正方形ABC′D′,
∴点D′的横坐标为3,
∴当x=3时,y=$\frac{2}{3}$,
∴点E的坐标为(3,$\frac{2}{3}$).
点评 本题主要考查反比例函数图象上点的坐标特征,熟练掌握轴对称的性质、翻折的性质及待定系数法求函数解析式是解题的关键.

练习册系列答案
相关题目
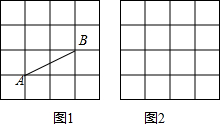 如图1,图2,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点.图1中的线段AB的两个端点都在格点上.
如图1,图2,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点.图1中的线段AB的两个端点都在格点上. 如图,一个长方形推拉窗,窗高1.5m,则活动窗的通风面积S(m2)与拉开长度b(m)的关系式是S=1.5b.
如图,一个长方形推拉窗,窗高1.5m,则活动窗的通风面积S(m2)与拉开长度b(m)的关系式是S=1.5b. 已知:如图,在?ABCD中,E、F是对角线BD上的两点,BE=DF,求证:AE=CF.
已知:如图,在?ABCD中,E、F是对角线BD上的两点,BE=DF,求证:AE=CF.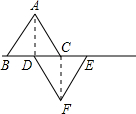 如图,已知△ABC和△DEF是两个边长都为1cm的等边三角形,且B、D、C、E都在同一直线上,连接AD、CF.
如图,已知△ABC和△DEF是两个边长都为1cm的等边三角形,且B、D、C、E都在同一直线上,连接AD、CF. 如图,四边形ABCD是平行四边形,E,F分别为BC,AD的中点,
如图,四边形ABCD是平行四边形,E,F分别为BC,AD的中点,