题目内容
14. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点B的对应点D的坐标为( )
如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点B的对应点D的坐标为( )| A. | (3,3) | B. | (1,4) | C. | (3,1) | D. | (4,1) |
分析 利用位似图形的性质,结合两图形的位似比,进而得出D点坐标.
解答 解:∵线段AB的两个端点坐标分别为A(6,6),B(8,2),
以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,
∴点D的横坐标和纵坐标都变为B点的一半,
∴点D的坐标为:(4,1).
故选:D.
点评 此题主要考查了位似图形的性质,利用两图形的位似比得出对应点横纵坐标关系是解题关键.在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
19.若∠α与∠β互余,且∠α:∠β=3:2,那么∠α与∠β的度数分别是( )
| A. | 36°,54° | B. | 60°,40° | C. | 54°,36° | D. | 72°,108° |
6.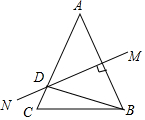 如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是( )
如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是( )
 如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是( )
如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是( )| A. | 50° | B. | 45° | C. | 55° | D. | 60° |
 如图,AB∥CD,∠B=61°,∠D=35°.求∠1和∠A的度数.
如图,AB∥CD,∠B=61°,∠D=35°.求∠1和∠A的度数. (1)如图:A、B、C、D四点在同一直线上,若AB=CD.
(1)如图:A、B、C、D四点在同一直线上,若AB=CD.