Question

9．（1）如图：A、B、C、D四点在同一直线上，若AB=CD．
①图中共有6条线段；
②比较线段的大小：AC=BD（填“＞”、“=”或“＜”）；
③若BC=$\frac{2}{3}$AC，且AC=6cm，则AD的长为8cm；
（Ⅱ）已知线段AB=8cm，在直线AB上有一点C，且BC=4cm，点M是线段AC的中点，求线段AM的长．

Answer 1

分析 （1）①每两个点作为线段的端点，即任取其中的两点即可得到一条线段，可以得出共有6条；
②由线段AB=CD得出AB+BC=CD+BC，即可得出结论；
③由已知求出BC的长，得出CD的长，即可得出AD的长；
（Ⅱ）根据线段的和差，可得线段AC的长，再根据线段中点的性质，可得答案．

解答 解：①任取其中两点作为线段的端点，则可以得到的线段为：AB、AC、AD、BC、BD、CD，共有6条；
故答案为：6．
②∵AB=CD，
∴AB+BC=CD+BC，
∴AC=BD；
故答案为：=；
③∵BC=$\frac{2}{3}$AC，且AC=6cm，
∴BC=4cm，
∴AB=CD=AC-BC=2cm，
∴AD=AC+CD=8cm；
故答案为：8；
（Ⅱ）：如图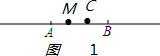，当C在线段AB上时，由线段的和差，得
AC=AB-BC=8-4=4（cm），
由M是线段AC的中点，得
AM=$\frac{1}{2}$AC=$\frac{1}{2}$×4=2（cm）；
如图2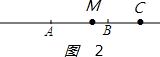，当C在线段AB的延长线上时，由线段的和差，得
AC=AB+BC=8+4=12（cm），
由M是线段AC的中点，得
AM=$\frac{1}{2}$AC=$\frac{1}{2}$×12=6（cm）；
综上所述：AM的长为2cm或6cm．

点评 本题考查了两点间的距离、线段的中点的定义以及线段的和差；注意（Ⅱ）分类讨论．