题目内容
2.已知|3a+1|+$\sqrt{b-1}$=0,则-a2-b2015=-$\frac{10}{9}$.分析 根据非负数的性质列式求出a、b的值,然后代入代数式进行计算即可得解.
解答 解:由题意得,3a+1=0,b-1=0,
解得a=-$\frac{1}{3}$,b=1,
所以,-a2-b2015=-(-$\frac{1}{3}$)2-12015=-$\frac{1}{9}$-1=-$\frac{10}{9}$.
故答案为:-$\frac{10}{9}$.
点评 本题考查了非负数的性质:有限个非负数的和为零,那么每一个加数也必为零.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.化简(3-a)$•\sqrt{\frac{1}{a-3}}$,得( )
| A. | $\sqrt{3-a}$ | B. | $\sqrt{a-3}$ | C. | -$\sqrt{3-a}$ | D. | -$\sqrt{a-3}$ |
17.用-x表示的数一定是( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 无法确定 |
14.下列各组数中,不是勾股数的是( )
| A. | 3,4,5 | B. | 5,12,13 | C. | 8,15,17 | D. | 10,15、18 |
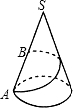 已知圆锥底面半径r=10cm,母线SA长为40cm.一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是20$\sqrt{5}$cm.
已知圆锥底面半径r=10cm,母线SA长为40cm.一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是20$\sqrt{5}$cm.