题目内容
9.若点(-2,y1),(-1,y2),(6,y3)在反比例函数y=$\frac{2015}{x}$的图象上,则y1、y2、y3的大小关系是y3>y1>y2.(用“>”连接)分析 由反比例函数图象上点的坐标特征找出y1、y2、y3的值,进行比较后即可得出结论.
解答 解:令反比例函数y=$\frac{2015}{x}$中x=-2,则y1=-$\frac{2015}{2}$,
令反比例函数y=$\frac{2015}{x}$中x=-1,则y2=-2015,
令反比例函数y=$\frac{2015}{x}$中x=6,则y3=$\frac{2015}{6}$.
∵$\frac{2015}{6}$>-$\frac{2015}{2}$>-2015,
∴y3>y1>y2.
故答案为:y3>y1>y2.
点评 本题考查了反比例函数图象上点的坐标特征,解题的关键是找出y1、y2、y3的值.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数图象上点的坐标特征找出y1、y2、y3的值是关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
15.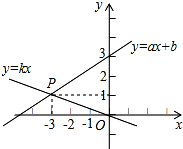 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是( )
如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是( )
 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是( )
如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是( )| A. | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ |
 如图所示的几何体由7个大小相同的小正方体紧密摆放而成,且每个小正方体的棱长均为1,则这个几何体主视图的面积为6.
如图所示的几何体由7个大小相同的小正方体紧密摆放而成,且每个小正方体的棱长均为1,则这个几何体主视图的面积为6. 如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=35°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转25°.
如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=35°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转25°.