题目内容
5.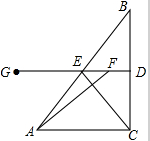 如图,在Rt△ABC中,∠ACB=90°,AC=4cm,动点F在线段BC的垂直平分线DG上,垂足为D,DG交AB于E,连接CE,AF,动点F从D点出发以1cm/s的速度移动,设运动时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,AC=4cm,动点F在线段BC的垂直平分线DG上,垂足为D,DG交AB于E,连接CE,AF,动点F从D点出发以1cm/s的速度移动,设运动时间为t(s).(1)当t=6s时,求证:四边形ACEF是平行四边形;
(2)①在(1)的条件下,当∠B=30°时,四边形ACEF是菱形;
②当t=4s时,四边形ACDF是矩形.
分析 (1)根据垂直平分线的性质找出∠BDE=∠BCA=90°,进而得出DE∥AC,再根据三角形中位线的性质可得出DE的长度,根据边与边之间的关系可得出EF=AC,从而可证出四边形ACEF是平行四边形;
(2)①根据垂直平分线的性质可得出BE=EC=$\frac{1}{2}$AB,再根据菱形的性质可得出AC=CE=$\frac{1}{2}$AB,利用特殊角的正弦值即可得出∠B的度数;
②根据矩形的性质可得出DF=AC,再根据运动时间=路程÷速度即可得出结论.
解答 (1)证明:当t=6时,DF=6cm.
∵DG是BC的垂直平分线,∠ACB=90°,
∴∠BDE=∠BCA=90°,
∴DE∥AC,DE为△BAC的中位线,
∴DE=$\frac{1}{2}$AC=2.
∵EF=DF-DE=4=AC,EF∥AC,
∴四边形ACEF是平行四边形.
(2)①∵DG是BC的垂直平分线,
∴BE=EC=$\frac{1}{2}$AB,
∵四边形ACEF是菱形,
∴AC=CE=$\frac{1}{2}$AB,
∴sin∠B=$\frac{AC}{AB}$=$\frac{1}{2}$,
∴∠B=30°.
故答案为:30°.
②∵四边形ACDF是矩形,
∴DF=AC=4,
∵动点F从D点出发以1cm/s的速度移动,
∴t=4÷1=4(秒).
故答案为:4.
点评 本题考查了平行四边形的判定、菱形的性质、特殊角的三角函数值以及矩形的性质,解题的关键是:(1)找出EF=AC,且EF∥AC;(2)①找出sin∠B=$\frac{AC}{AB}$=$\frac{1}{2}$;②根据数量关系算出时间t.本题属于中档题,难度不大,解决该题型题目时,根据平行四边形(菱形或矩形)的性质找出相等的边角关系是关键.

练习册系列答案
相关题目
16.在下列说法中正确的是( )
| A. | 在 Rt△ABC中,AB2+BC2=AC2 | |
| B. | 在 Rt△ABC中,若a=3,b=4,则c=5 | |
| C. | 在 Rt△ABC中,两直角边长都为15,则斜边长为$\sqrt{450}$ | |
| D. | 在直角三角形中,若斜边长为10,则可求出两直角边的长 |
13.体育课上,老师测量跳远成绩的依据是( )
| A. | 垂直的定义 | B. | 两点之间线段最短 | ||
| C. | 垂线段最短 | D. | 两点确定一条直线 |
20.方程组$\left\{\begin{array}{l}{2x-y=5}\\{3x+4y=2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ |
14.下列运算正确的是( )
| A. | 3$\sqrt{2}$-$\sqrt{2}$=3 | B. | a6÷a3=a2 | C. | a2+a3=a5 | D. | (3a3)2=9a6 |
15.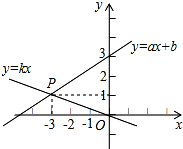 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是( )
如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是( )
 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是( )
如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是( )| A. | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ |
 如图所示的几何体由7个大小相同的小正方体紧密摆放而成,且每个小正方体的棱长均为1,则这个几何体主视图的面积为6.
如图所示的几何体由7个大小相同的小正方体紧密摆放而成,且每个小正方体的棱长均为1,则这个几何体主视图的面积为6.