题目内容
6．已知一个菱形的两条对角线的长度分别为6和8，那么这个菱形的周长是20．分析 首先根据题意画出图形，由四边形ABCD是菱形，对角线AC=6，BD=8，则可求得OA，OB的长，然后由勾股定理即可求得边AB的长，继而求得答案．
解答 解：∵四边形ABCD是菱形，
∴AB=BC=CD=AD，
OA=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3，
OB=$\frac{1}{2}$BD=$\frac{1}{2}$×8=4，AC⊥BD，
在Rt△OAB中，AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5，
∴菱形ABCD的周长为：5×4=20．
故答案为：20．
点评 此题考查了菱形的性质，解答本题的关键是掌握菱形的对角线互相垂直且平分，属于基础题，难度一般．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
14．下列运算正确的是（ ）
| A． | 3$\sqrt{2}$-$\sqrt{2}$=3 | B． | a6÷a3=a2 | C． | a2+a3=a5 | D． | （3a3）2=9a6 |
15．
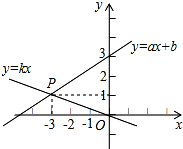如图，已知函数y=ax+b和y=kx的图象交于点P，则根据图象可得，关于x、y的二元一次方程组的解是（ ）
如图，已知函数y=ax+b和y=kx的图象交于点P，则根据图象可得，关于x、y的二元一次方程组的解是（ ）| A． | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ |
如图，直线a与直线b交于点A，与直线c交于点B，∠1=120°，∠2=35°，若使直线b与直线c平行，则可将直线b绕点A逆时针旋转25°．