题目内容
7．
已知二次函数y=$\frac{1}{2}$x2-x-$\frac{3}{2}$．（1）用配方法求该二次函数的图象的顶点坐标；
（2）在右图中画出该函数图象；
（3）观察图象后判断，当x满足什么值时，y＞0？
分析 （1）用配方法把一般式化为顶点式，根据二次函数的性质，求出顶点坐标；
（2）根据函数性质：开口方向、对称轴、顶点坐标和与坐标轴的交点，画出图象；
（3）观察图象，求出x满足的条件．
解答 解：（1）y=$\frac{1}{2}$（x-1）2-2，顶点坐标为（1，-2）
（2）由解析式可知，开口向上，对称轴为x=1，顶点坐标为（1，-2），与y轴交点为（0，-$\frac{3}{2}$），与x轴的交点为（-1，0）（3，0）
所以图象为：
（3）从图象可知，x＜-1或x＞3时，y＞0．
点评 本题考查的是配方法求顶点坐标、画函数图象以及根据图象解决问题，掌握配方法、根据函数性质画图象和读懂图象信息是解题的关键，注意数形结合思想的灵活运用．
练习册系列答案
相关题目
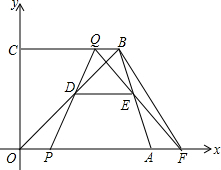如图，在直角梯形OABC中，OA∥CB，A、B两点的坐标分别为A（15，0），B（10，12），动点P、Q分别从O、B出发，点P以每秒2个单位长度的速度沿OA向终点A运动，点Q以每秒1个单位的速度沿BC向终点C运动，当点P停止运动时，点Q也同时停止运动．线段OB、PQ相交于点D，过点D作DE∥OA，交AB于点E，连接QE并延长，交x轴于点F．设动点P、Q的运动时间为t（单位：秒）
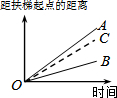
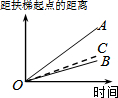
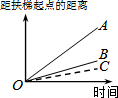
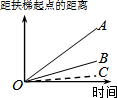
在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA边上的中点，阅读下列材料，回答问题：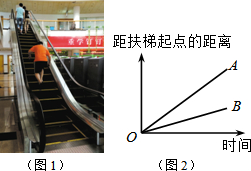
大明因急事在运行中的自动扶梯上行走去二楼（如图1），图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时，距自动扶梯起点的距离与时间之间的关系．下面四个图中，虚线OC能大致表示大明在停止运行（即静止）的自动扶梯上行走去二楼时，距自动扶梯起点的距离与时间关系的是（ ）
