题目内容
18．若把代数式x2+2bx+4化为（x-m）2+k的形式，其中m，k为常数，则k-m的最大值是$\frac{17}{4}$．分析 首先把代数式x2+2bx+4变为x2+2bx+b2-b2+4，再进一步利用完全平方公式，把前三项因式分解化为（x-m）2+k的形式，求出m、k的数值即可．
解答 解：x2+2bx+4
=x2+2bx+b2-b2+4
=（x+b）2-b2+4；
∴m=-b，k=-b2+4，
则k-m=-（b-$\frac{1}{2}$）2+$\frac{17}{4}$．
∵-（b-$\frac{1}{2}$）2≤0，
∴当b=$\frac{1}{2}$时，k-m的最大值是$\frac{17}{4}$．
故答案为：$\frac{17}{4}$．
点评 此题考查利用完全平方公式配方，注意代数式的恒等变形．
练习册系列答案
相关题目
如图所示，在△ABC中，∠C=135°，BC=$\sqrt{2}$，AC=2，求AB的长．
9．
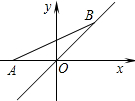如图，点A的坐标为（-2，0），点B在直线y=x上运动，当线段AB最短时点B的坐标为（ ）
如图，点A的坐标为（-2，0），点B在直线y=x上运动，当线段AB最短时点B的坐标为（ ）| A． | （0，0） | B． | （-1，-1） | C． | （$\sqrt{2}$，-$\sqrt{2}$） | D． | （-$\sqrt{2}$，-$\sqrt{2}$） |
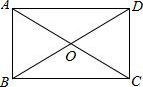如图，在矩形ABCD中，AB比AD的一半长2cm，AD=10cm，问△ABD的周长比△AOD的周长长多少？
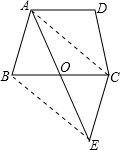如图，梯形ABCD中，AD∥BC，AB=AD=DC，O是BC中点，将△ABO绕点O旋转180°至△ECO．