题目内容
2.P表示n边形对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么P与n的关系式是P=$\frac{n(n-1)}{24}$(n2-an+b)(其中a,b是常数,n≥4)
(1)填空:通过画图可得:
四边形时,P=1(填数字);五边形时,P=5(填数字)
(2)请根据四边形和五边形对角线的交点个数,结合关系式,求a和b的值.(注:本题中的多边形均指凸多边形)
分析 (1)根据题意画出图形,进而得出四边形和五边形中P的值;
(2)利用(1)中所求,得出二元一次方程组进而求出即可.
解答  解:(1)如图所示:四边形时,P=1;五边形时,P=5;
解:(1)如图所示:四边形时,P=1;五边形时,P=5;
故答案为:1,5;
(2)由(1)得:$\left\{\begin{array}{l}{\frac{4(4-1)}{24}({4}^{2}-4a+b)=1}\\{\frac{5(5-1)}{24}({5}^{2}-5a+b)=5}\end{array}\right.$,
整理得:$\left\{\begin{array}{l}{4a-b=14}\\{5a-b=19}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=5}\\{b=6}\end{array}\right.$.
点评 此题主要考查了二元一次方程组的应用,根据题意得出正确关于a,b的等量关系是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.下列数据是2015年4月5日10时公布的中国六大城市的空气污染指数情况:
则这组数据的中位数和众数分别是( )
| 城市 | 天津 | 合肥 | 南京 | 贵阳 | 成都 | 南昌 |
| 污染指数 | 342 | 163 | 165 | 45 | 227 | 163 |
| A. | 185和163 | B. | 164和163 | C. | 185和164 | D. | 163和164 |
11.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的大小为( )
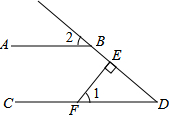

| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
12. 下列主视图正确的是( )
下列主视图正确的是( )
 下列主视图正确的是( )
下列主视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
 如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=$\frac{\sqrt{6}+\sqrt{2}}{2}$,则正方形的面积为4.
如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=$\frac{\sqrt{6}+\sqrt{2}}{2}$,则正方形的面积为4. 如图,△ABC中,∠ABC=90°,F是AC的中点,过AC上一点D作DE∥AB,交BF的延长线于点E,AG⊥BE,垂足是G,连接BD、AE.
如图,△ABC中,∠ABC=90°,F是AC的中点,过AC上一点D作DE∥AB,交BF的延长线于点E,AG⊥BE,垂足是G,连接BD、AE.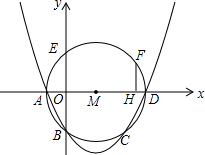 如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(-1,0),(0,-2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧$\widehat{ED}$上的点F作FH⊥AD于点H,且FH=1.5
如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(-1,0),(0,-2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧$\widehat{ED}$上的点F作FH⊥AD于点H,且FH=1.5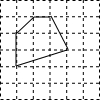 如图,多边形的各顶点都在方格纸的格点(横竖格子线的交错点)上,这样的多边形称为格点多边形,它的面积S可用公式S=a+$\frac{1}{2}$b-1(a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克定理”.现用一张方格纸共有200个格点,画有一个格点多边形,它的面积S=40.
如图,多边形的各顶点都在方格纸的格点(横竖格子线的交错点)上,这样的多边形称为格点多边形,它的面积S可用公式S=a+$\frac{1}{2}$b-1(a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克定理”.现用一张方格纸共有200个格点,画有一个格点多边形,它的面积S=40.