题目内容
12.对于任意两个正数m、n,定义运算*为:m*n=$\left\{\begin{array}{l}{\sqrt{m}-\sqrt{n}(m≥n)}\\{\sqrt{m}+\sqrt{n}(m<n)}\end{array}\right.$
计算(8※3)×(18※27)的结果为3+3$\sqrt{6}$.
分析 利用新定义得到(8※3)×(18※27)=($\sqrt{8}$-$\sqrt{3}$)($\sqrt{18}$+$\sqrt{27}$),再把二次根式化为最简二次根式,然后利用乘法公式展开后合并即可.
解答 解:(8※3)×(18※27)=($\sqrt{8}$-$\sqrt{3}$)($\sqrt{18}$+$\sqrt{27}$)
=(2$\sqrt{2}$-$\sqrt{3}$)(3$\sqrt{2}$+3$\sqrt{3}$)
=12+6$\sqrt{6}$-3$\sqrt{6}$-9
=3+3$\sqrt{6}$.
故答案为3+3$\sqrt{6}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
3.已知c>1,a=$\sqrt{c+1}$-$\sqrt{c}$,b=$\sqrt{c}$-$\sqrt{c-1}$,则a、b的大小关系是( )
| A. | a>b | B. | a≥b | C. | a<b | D. | a≤b |
17.若$\sqrt{10201}$=101,则$\sqrt{102.01}$等于( )
| A. | 1.01 | B. | 10.1 | C. | 101 | D. | 1.0201 |
4.桥梁上的拉杆,电视塔的底座,都是三角形结构,而活动挂架是四边形结构,这是分别利用三角形和四边形的( )
| A. | 稳定性,稳定性 | B. | 稳定性,不稳定性 | ||
| C. | 不稳定性,稳定性 | D. | 不稳定性,不稳定性 |
2.在平面直角坐标系xOy中,⊙O的半径为4,点P的坐标为(3,4),则点P的位置为( )
| A. | 在⊙O外 | B. | 在⊙O上 | C. | 在⊙O内 | D. | 不确定 |




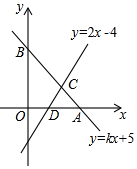 已知直线y=kx+5交x轴于A,交y轴于B且A坐标为(5,0),直线y=2x-4与x轴于D,与直线AB相交于点C.
已知直线y=kx+5交x轴于A,交y轴于B且A坐标为(5,0),直线y=2x-4与x轴于D,与直线AB相交于点C.