题目内容
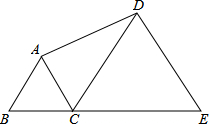 如图,△ABC与△DCE都是等边三角形,B,C,E三点在同一条直线上,若AB=3,∠BAD=150°,则DE的长为( )
如图,△ABC与△DCE都是等边三角形,B,C,E三点在同一条直线上,若AB=3,∠BAD=150°,则DE的长为( )| A、3 | B、4 | C、5 | D、6 |
考点:含30度角的直角三角形,等边三角形的性质
专题:
分析:根据等边三角形的性质得出AB=AC=3,DE=DC,∠BAC=∠DCE=∠ACB=60°,求出∠ACD=60°,∠CAD=90°,求出∠ADC=30°,根据很30度角的直角三角形性质得出DC=2AC,求出即可.
解答:解:∵△ABC与△DCE都是等边三角形,AB=3,∠BAD=150°,
∴AB=AC=3,DE=DC,∠BAC=∠DCE=∠ACB=60°,
∴∠ACD=60°,∠CAD=150°-60°=90°,
∴∠ADC=30°,
∴DC=2AC=6,
∴DE=DC=6,
故选D.
∴AB=AC=3,DE=DC,∠BAC=∠DCE=∠ACB=60°,
∴∠ACD=60°,∠CAD=150°-60°=90°,
∴∠ADC=30°,
∴DC=2AC=6,
∴DE=DC=6,
故选D.
点评:本题考查了等边三角形的性质和含30度角的直角三角形性质,三角形内角和定理的应用,解此题的关键是得出DC=2AC.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
 如图已知:在△ABC中,AB=AC,点D在BC边上,且BD=CD,求证:AD平分∠BAC.
如图已知:在△ABC中,AB=AC,点D在BC边上,且BD=CD,求证:AD平分∠BAC. 如图,△ABC的是三个顶点都在⊙O上,AB=AC,∠BAC=120°,BD为⊙O直径,且AD=6,求AB的长.
如图,△ABC的是三个顶点都在⊙O上,AB=AC,∠BAC=120°,BD为⊙O直径,且AD=6,求AB的长.