题目内容
9.若关于x,y的二元一次方程组$\left\{\begin{array}{l}y-\frac{1}{2}x=-1\\ y+x=5\end{array}\right.$的解是$\left\{\begin{array}{l}x=4\\ y=1\end{array}\right.$,则直线$y=\frac{1}{2}x-1$与y=-x+5的交点坐标为( )| A. | (4,1) | B. | (1,4) | C. | (-4,1) | D. | (2,1) |
分析 二元一次方程可以化为一次函数,两个二元一次方程组的解就是两个函数的交点坐标.
解答 解:∵二元一次方程组$\left\{\begin{array}{l}y-\frac{1}{2}x=-1\\ y+x=5\end{array}\right.$的解是$\left\{\begin{array}{l}x=4\\ y=1\end{array}\right.$,
∴直线$y=\frac{1}{2}x-1$与y=-x+5的交点坐标为(4,1).
故选A.
点评 本题主要考查了一次函数与二元一次方程组,满足解析式的点就在函数的图象上,在函数图象上的点,就一定满足函数解析式.函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
相关题目
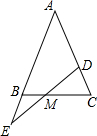 在等腰三角形ABC的腰AC上取一点D,腰AB的延长线上取一点E,使CD=BE,交BC于M,探索能得到的结论,并证明.
在等腰三角形ABC的腰AC上取一点D,腰AB的延长线上取一点E,使CD=BE,交BC于M,探索能得到的结论,并证明.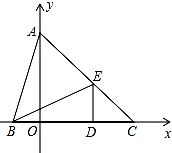 如图,在平面直角坐标系中,点A(0,b),点B(a,0),点D(d,0),其中a、b、d满足$\sqrt{a+1}$+|b-3|+(2-d)2=0,DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.
如图,在平面直角坐标系中,点A(0,b),点B(a,0),点D(d,0),其中a、b、d满足$\sqrt{a+1}$+|b-3|+(2-d)2=0,DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C. 如图,等腰△ABC中,AB=AC,∠C=65°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是15°.
如图,等腰△ABC中,AB=AC,∠C=65°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是15°. 如图,一次函数y=kx+b的图象经过点A(0,2),点B(1,0),则不等式kx+b<0的解集为x>1.
如图,一次函数y=kx+b的图象经过点A(0,2),点B(1,0),则不等式kx+b<0的解集为x>1.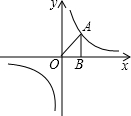 如图所示,A为反比例函数$y=\frac{k}{x}$图象上一点,AB垂直x轴,垂足为B点,若S△AOB=3,则k的值为6.
如图所示,A为反比例函数$y=\frac{k}{x}$图象上一点,AB垂直x轴,垂足为B点,若S△AOB=3,则k的值为6.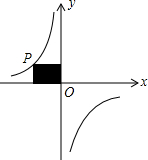 如图,P是反比例函数y=$\frac{k}{x}$的图象上的一点,过点P分别作x轴、y轴的垂线,得图中阴影部分的面积为6,则这个反比例函数的比例系数是-6.
如图,P是反比例函数y=$\frac{k}{x}$的图象上的一点,过点P分别作x轴、y轴的垂线,得图中阴影部分的面积为6,则这个反比例函数的比例系数是-6.