题目内容
7.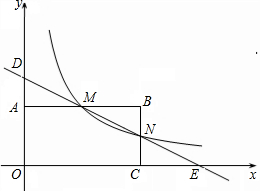 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(-8,4).过点D(0,6)和E(12,0)的直线分别与AB,BC交于点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(-8,4).过点D(0,6)和E(12,0)的直线分别与AB,BC交于点M,N.(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数y=$\frac{m}{x}$(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(3)若反比例函数y=$\frac{m}{x}$(x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
分析 (1)设直线DE的解析式为y=kx+b,直接把点D,E代入解析式利用待定系数法即可求得直线DE的解析式,先根据矩形的性质求得点M的纵坐标,再代入一次函数解析式求得其横坐标即可;
(2)利用点M求得反比例函数的解析式,根据一次函数求得点N的坐标,再代入反比例函数的解析式判断是否成立即可;
(3)满足条件的最内的双曲线的m=16,最外的双曲线的m=32,所以可得其取值范围.
解答 解:(1)设直线DE的解析式为y=kx+b(k≠0),
∵点D,E的坐标为(0,6)、(12,0),
∴$\left\{\begin{array}{l}b=6\\ 12k+b=0\end{array}\right.$,解得$\left\{\begin{array}{l}b=6\\ k=-\frac{1}{2}\end{array}\right.$,
∴直线DE的解析式为y=-$\frac{1}{2}$x+6.
∵点M在AB边上,B(8,4),而四边形OABC是矩形,
∴点M的纵坐标为4;
又∵点M在直线y=-$\frac{1}{2}$x+6上,
∴4=-$\frac{1}{2}$x+6;
∴x=4;
∴M(4,4);
(2)∵y=$\frac{m}{x}$(x>0)经过点M(4,4),
∴m=16;
∴y=$\frac{16}{x}$;
又∵点N在BC边上,B(8,4),
∴点N的横坐标为8.
∵点N在直线y=-$\frac{1}{2}$x+6上,
∴y=2;
∴N(8,2);
∵当x=8时,y=$\frac{16}{x}$=2,
∴点N在函数y=$\frac{16}{x}$的图象上;
(3)当反比例函数y=$\frac{m}{x}$(x>0)的图象通过点M(4,4),N(8,2)时m的值最小,当反比例函数y=$\frac{m}{x}$(x>0)的图象通过点B(8,4)时m的值最大,
∴4=$\frac{m}{4}$,有m的值最小为16,
4=$\frac{m}{8}$,有m的值最大为32,
∴16≤m≤32.
点评 此题综合考查了反比例函数综合题,涉及到一次函数的性质,此题难度稍大,综合性比较强,注意反比例函数上的点与反比例函数的k值之间的关系,并会根据函数解析式和点的坐标验证某个点是否在函数图象上.

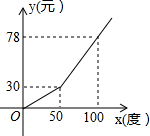 某地电力公司的用电收费标准如图,x(度)表示用户每月的用电量,y(元)表示每月应付的电费,看图可知,当用户一个月的用电量超过50度时,超过部分的收费标准是每度( )
某地电力公司的用电收费标准如图,x(度)表示用户每月的用电量,y(元)表示每月应付的电费,看图可知,当用户一个月的用电量超过50度时,超过部分的收费标准是每度( )| A. | 0.96元 | B. | 0.78元 | C. | 0.60元 | D. | 0.3元 |
| A. | 平行四边形的对角顶点关于对角线交点对称 | |
| B. | 平行四边形的对边关于对角线交点对称 | |
| C. | 线段、矩形、平行四边形既是轴对称图形,也是中心对称图形 | |
| D. | 关于中心对称的两个图形,对应线段平行且相等 |
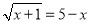 的解是( )
的解是( )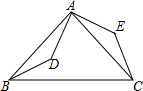 如图,点D是等腰直角三角形ABC内一点,AB=AC,将△ABD绕点A逆时针旋转90°,点D与点E重合,则△ABD≌△ACE;若连结DE,AD=3,则DE=3$\sqrt{2}$.
如图,点D是等腰直角三角形ABC内一点,AB=AC,将△ABD绕点A逆时针旋转90°,点D与点E重合,则△ABD≌△ACE;若连结DE,AD=3,则DE=3$\sqrt{2}$. 如图,在△ABC中,∠B=60°,AD平分∠BAC交BC于D,若AB+BD=AC,那么∠C=30度.
如图,在△ABC中,∠B=60°,AD平分∠BAC交BC于D,若AB+BD=AC,那么∠C=30度.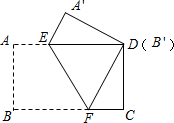 把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,则重叠部分△DEF的面积?
把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,则重叠部分△DEF的面积?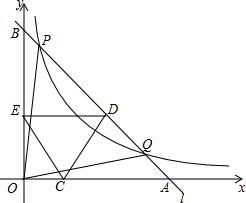 如图,已知双曲线y=$\frac{k}{x}(x>0)$与经过点A(1,0),B(0,1)的直线交于P,Q两点,且P的横坐标与Q的纵坐标都是$\frac{1}{4}$,连接OP,OQ.
如图,已知双曲线y=$\frac{k}{x}(x>0)$与经过点A(1,0),B(0,1)的直线交于P,Q两点,且P的横坐标与Q的纵坐标都是$\frac{1}{4}$,连接OP,OQ.