题目内容
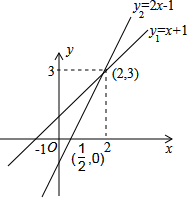 已知y1=k1x+b1,y2=k2x+b2.定义函数y=y1•y2=(k1x+b1)(k2x+b2).
已知y1=k1x+b1,y2=k2x+b2.定义函数y=y1•y2=(k1x+b1)(k2x+b2).(1)若y1=x+1,y2=2x-1两函数图象如图,观察图象并指出:当x取何值时,y=0; 当x的取值在什么范围时,y>0.
(2)若y=x2-x-6,求当x的取值在什么范围时,y≥0.
(3)若定义函数y=
| y1 |
| y2 |
考点:两条直线相交或平行问题
专题:
分析:(1)当x+1和2x-1中只要有一个等于0,则y=0成立,当x+1和2x-1同号时,y>0成立;
(2)把y=x2-x-6写成两个一次式的乘积,即可根据(1)的解法求解;
(3)y<0,则x+1和2x-1一定异号,根据图象即可求解.
(2)把y=x2-x-6写成两个一次式的乘积,即可根据(1)的解法求解;
(3)y<0,则x+1和2x-1一定异号,根据图象即可求解.
解答:解:(1)y1=x+1,y2=2x-1与x轴的交点坐标是((-1,0)和(
,0),则当x=-1或
时,y=0;
当x>
时,x+1>0且2x-1>0,此时y>0,当x<-1时,x+1<0且2x-1<0,此时y>0.
则当x>
或x<-1时,y>0;
(2)y=x2-x-6=(x-3)(x+2),
当x-3≥0且x+2≥0时,即x≥3时,y≥0,
当x-3≤0且x+2≤0时,即x≤-2时,y≥0.
则x≥3或x≤-2时,y≥0;
(3)当x+1和2x-1异号时,即-1<x<
时,y<0.
| 1 |
| 2 |
| 1 |
| 2 |
当x>
| 1 |
| 2 |
则当x>
| 1 |
| 2 |
(2)y=x2-x-6=(x-3)(x+2),
当x-3≥0且x+2≥0时,即x≥3时,y≥0,
当x-3≤0且x+2≤0时,即x≤-2时,y≥0.
则x≥3或x≤-2时,y≥0;
(3)当x+1和2x-1异号时,即-1<x<
| 1 |
| 2 |
点评:考查了两条直线相交或平行问题,本题要求利用图象求解各问题,要认真体会点的坐标,一次函数与一元一次方程组之间的内在联系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在矩形ABCD中,AD=12cm,AB=acm,三角形的直角形顶点P在线段BC上,一直角边与线段AD的交点为Q,另一直角边与线段AB的交点为E,点P从C开始向B以2cm/s的速度运动,点Q从D开始以1cm/s的速度向点A运动,假设P、Q两点开始运动,运动时间为ts.
如图,在矩形ABCD中,AD=12cm,AB=acm,三角形的直角形顶点P在线段BC上,一直角边与线段AD的交点为Q,另一直角边与线段AB的交点为E,点P从C开始向B以2cm/s的速度运动,点Q从D开始以1cm/s的速度向点A运动,假设P、Q两点开始运动,运动时间为ts.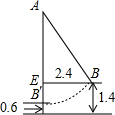 如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B离地面0.6米,荡秋千到AB的位置时,下端B距静止位置的水平距离EB,等于2.4米,距地面1.4米,求秋千AB的长.
如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B离地面0.6米,荡秋千到AB的位置时,下端B距静止位置的水平距离EB,等于2.4米,距地面1.4米,求秋千AB的长. 如图,直线y=-x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
如图,直线y=-x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.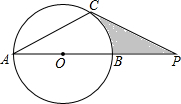 如图,⊙O的直径AB与弦AC的夹角∠A=30°,过点C作⊙O的切线交AB的延长线于点P,PC=
如图,⊙O的直径AB与弦AC的夹角∠A=30°,过点C作⊙O的切线交AB的延长线于点P,PC=