题目内容
20. 如图,已知正方形ABCD的边长为12,E是BC的中点,将△DEC沿DE折叠到△DEF,
如图,已知正方形ABCD的边长为12,E是BC的中点,将△DEC沿DE折叠到△DEF,延长EF交AB于G,连接DG
(1)BE=6;
(2)EG=10.
分析 (1)根据线段中点的概念解答;
(2)根据翻转变换的性质得到DF=DC=AD,∠DFE=∠C=90°,证明Rt△DGA≌Rt△DGF,得到GA=GF,根据勾股定理计算即可.
解答 解:(1)∵正方形ABCD的边长为12,E是BC的中点,
∴BE=$\frac{1}{2}$BC=6,
故答案为:6;
(2)由翻转变换的性质可知,DF=DC=AD,∠DFE=∠C=90°,
在Rt△DGA和Rt△DGF中,
$\left\{\begin{array}{l}{DA=DF}\\{DG=DG}\end{array}\right.$,
∴Rt△DGA≌Rt△DGF,
∴GA=GF,
由勾股定理得,BG2+BE2=GE2,即(12-GA)2+62=(6+GA)2,
解得,GA=2,
则EG=GF+FE=10,
故答案为:10.
点评 本题考查的是翻转变换的性质,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.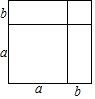 如图,能根据图形中的面积说明的乘法公式是( )
如图,能根据图形中的面积说明的乘法公式是( )
 如图,能根据图形中的面积说明的乘法公式是( )
如图,能根据图形中的面积说明的乘法公式是( )| A. | (a+b)(a-b)=a2-b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | (a-b)=a2-2ab+b2 | D. | (x+p)(x+q)=x2+(p+q)x+pq |
11. 如图,在等腰△ABC顶角A=36°,两底角的平分线BD、CE交于点F,则图中等腰三角形的个数为( )
如图,在等腰△ABC顶角A=36°,两底角的平分线BD、CE交于点F,则图中等腰三角形的个数为( )
 如图,在等腰△ABC顶角A=36°,两底角的平分线BD、CE交于点F,则图中等腰三角形的个数为( )
如图,在等腰△ABC顶角A=36°,两底角的平分线BD、CE交于点F,则图中等腰三角形的个数为( )| A. | 6个 | B. | 8个 | C. | 10个 | D. | 12个 |
15.已知线段CD是由线段AB平移得到的.若点A(-2,2)的对应点为C(3,-1),则点B(1,5)的对应点D的坐标为( )
| A. | (-4,8) | B. | (6,2) | C. | (-4,2) | D. | (4,-8) |
12.原命题为:“若a>0,b>0,则a+b>0”,逆命题为:“若a+b>0,则a>0,b>0”.下列判定正确的是( )
| A. | 原命题为真命题,逆命题为假命题 | B. | 原命题与逆命题均为真命题 | ||
| C. | 原命题为假命题,逆命题为真命题 | D. | 原命题与逆命题均为假命题 |
10. 如图,已知△ABC≌△BAD,F是AB的中点,则图中全等三角形共有( )
如图,已知△ABC≌△BAD,F是AB的中点,则图中全等三角形共有( )
 如图,已知△ABC≌△BAD,F是AB的中点,则图中全等三角形共有( )
如图,已知△ABC≌△BAD,F是AB的中点,则图中全等三角形共有( )| A. | 一组 | B. | 二组 | C. | 三组 | D. | 四组 |
 如图,点B到直线DC的距离是指线段BC的长度.
如图,点B到直线DC的距离是指线段BC的长度.