题目内容
1.解下列方程,选择适当的方法.(1)(3-x)2+x2=5
(2)x2+2$\sqrt{3}$x+3=0
(3)x2-2x=0
(4)x2+6x+9=7.
分析 (1)整理后分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(3)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(4)整理后求出b2-4ac的值,再代入公式求出即可.
解答 解:(1)(3-x)2+x2=5,
整理得:2x2-6x+4=0,
x2-3x+2=0,
(x-2)(x+1)=0,
x-2=0,x-1=0,
x1=2,x2=1;
(2)x2+2$\sqrt{3}$x+3=0,
(x+$\sqrt{3}$)2,
x+$\sqrt{3}=±$0,
x1=x2=-$\sqrt{3}$;
(3)x2-2x=0,
x(x-2)=0,
x=0,x-2=0,
x1=0,x2=2;
(4)x2+6x+9=7,
x2+6x+2=0,
b2-4ac=62-4×1×2=24,
x=$\frac{-6±\sqrt{24}}{2}$
x1=-3+$\sqrt{6}$,x2=-3-$\sqrt{6}$.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
相关题目
9.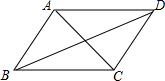 如图,在四边形ABCD中,给出下列的条件,能判断它是平行四边形的是( )
如图,在四边形ABCD中,给出下列的条件,能判断它是平行四边形的是( )
 如图,在四边形ABCD中,给出下列的条件,能判断它是平行四边形的是( )
如图,在四边形ABCD中,给出下列的条件,能判断它是平行四边形的是( )| A. | AB∥CD,AD=BC | B. | ∠B=∠C,∠A=∠D | C. | AB=AD,CB=CD | D. | AB=CD,AD=BC |
16.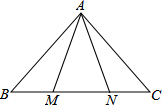 如图,∠B=50°,∠ANC=120°,AM=AN,则∠MAB的度数等于( )
如图,∠B=50°,∠ANC=120°,AM=AN,则∠MAB的度数等于( )
 如图,∠B=50°,∠ANC=120°,AM=AN,则∠MAB的度数等于( )
如图,∠B=50°,∠ANC=120°,AM=AN,则∠MAB的度数等于( )| A. | 10° | B. | 70° | C. | 60° | D. | 50° |
13.如图,它们是一个物体的三视图,该物体的形状是( )


| A. | 长方体 | B. | 正方体 | C. | 圆柱 | D. | 圆锥 |
 如图示,函数y=x+b和y=ax+3的图象交点为P,则不等式ax+3-x-b>0的解集为x<1.
如图示,函数y=x+b和y=ax+3的图象交点为P,则不等式ax+3-x-b>0的解集为x<1.