题目内容
14. 如图所示,铁路上A,B两站(视为直线上两点)相距14km,C,D为两村庄(可看为两个点),DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现要在铁路上建一个土特产品收购站E,使C,D两村到E站的距离相等,则E站应建在距A站多少km处?
如图所示,铁路上A,B两站(视为直线上两点)相距14km,C,D为两村庄(可看为两个点),DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现要在铁路上建一个土特产品收购站E,使C,D两村到E站的距离相等,则E站应建在距A站多少km处?
分析 在Rt△DAE和Rt△CBE中,设出AE的长,可将DE和CE的长表示出来,列出等式进行求解即可.
解答 解:设AE=xkm,
∵C、D两村到E站的距离相等,∴DE=CE,即DE2=CE2,
由勾股定理,得82+x2=62+(14-x)2,
解得:x=6.
故E点应建在距A站6千米处.
点评 本题主要考查了勾股定理的应用,运用勾股定理将两个直角三角形的斜边表示出来是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在正方形ABCD中,E在BC上,P在BD上,已知PA=PE,求证:PA⊥PE.
如图,在正方形ABCD中,E在BC上,P在BD上,已知PA=PE,求证:PA⊥PE.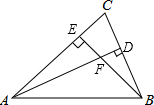 如图,已知△ABC的两条高AD、BE交于F,AE=BE,若要运用“HL”说明△AEF≌△BEC,还需添加条件:AF=BC.
如图,已知△ABC的两条高AD、BE交于F,AE=BE,若要运用“HL”说明△AEF≌△BEC,还需添加条件:AF=BC.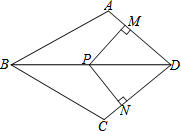 如图,在四边形ABCD中,DA=DC,P为对角线BD上一点,过点P作PM⊥AD,PN⊥CD,且PM=PN,
如图,在四边形ABCD中,DA=DC,P为对角线BD上一点,过点P作PM⊥AD,PN⊥CD,且PM=PN,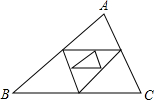 已知△ABC周长为1,连结△ABC三边中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,以此类推,第2014个三角形的周长为($\frac{1}{2}$)2013.
已知△ABC周长为1,连结△ABC三边中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,以此类推,第2014个三角形的周长为($\frac{1}{2}$)2013.