题目内容
4.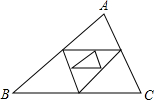 已知△ABC周长为1,连结△ABC三边中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,以此类推,第2014个三角形的周长为($\frac{1}{2}$)2013.
已知△ABC周长为1,连结△ABC三边中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,以此类推,第2014个三角形的周长为($\frac{1}{2}$)2013.
分析 根据三角形的中位线定理,找规律求解,每一条中位线均为其对应的边的长度的$\frac{1}{2}$,因此新三角形周长是前一个三角形周长的$\frac{1}{2}$.
解答 解:△ABC周长为1,
∵每条中位线均为其对应边的长度的$\frac{1}{2}$,
∴第2个三角形对应周长为$\frac{1}{2}$;
第3个三角形对应的周长为$\frac{1}{2}$×$\frac{1}{2}$=($\frac{1}{2}$)2;
第4个三角形对应的周长为$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$=($\frac{1}{2}$)3;
…
以此类推,第n个三角形对应的周长为($\frac{1}{2}$)n-1;
∴第2014个三角形对应的周长为($\frac{1}{2}$)2013.
故答案为:($\frac{1}{2}$)2013.
点评 此题考查了中位线定理;熟练掌握三角形中位线定理,找出每一个新的三角形周长是上一个三角形周长的$\frac{1}{2}$是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知两角及夹边作三角形,所用的基本作图方法是( )
| A. | 作已知角的平分线 | |
| B. | 作已知线段的垂直平分线 | |
| C. | 过一点作已知直线的高 | |
| D. | 作一个角等于已知角和作一条线段等于已知线段 |
 如图所示,铁路上A,B两站(视为直线上两点)相距14km,C,D为两村庄(可看为两个点),DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现要在铁路上建一个土特产品收购站E,使C,D两村到E站的距离相等,则E站应建在距A站多少km处?
如图所示,铁路上A,B两站(视为直线上两点)相距14km,C,D为两村庄(可看为两个点),DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现要在铁路上建一个土特产品收购站E,使C,D两村到E站的距离相等,则E站应建在距A站多少km处? 如图所示的抛物线是二次函数y=ax2-3x+a2-2的图象,那么a的值是-$\sqrt{2}$.
如图所示的抛物线是二次函数y=ax2-3x+a2-2的图象,那么a的值是-$\sqrt{2}$.


