题目内容
3.若直线$y=\frac{1}{2}x-2$与直线$y=-\frac{1}{4}x+a$相交于x轴上,则直线y=πx+a不经过( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 根据x轴上点的纵坐标为0,令y=0先求出交点坐标,再代入直线解析式求出a,然后根据一次函数的性质解答.
解答 解:令y=0,则$\frac{1}{2}$x-2=0,
解得x=4,
所以,两直线交点坐标为(4,0),
所以,-$\frac{1}{4}$×4+a=0,
解得a=1,
所以,直线y=πx+a为直线y=πx+1,
∵π>0,
∴直线经过第一三象限,
∵1>0,
∴直线与y轴的正半轴相交,
∴直线y=πx+a不经过第四象限.
故选D.
点评 本题考查了两直线相交问题,一次函数的性质,读懂题目信息求出两直线的交点是解题的关键.

练习册系列答案
相关题目
13.下列命题中,属于真命题的是( )
| A. | 两个锐角的和是锐角 | B. | 在同一平面内,如果a⊥b,b⊥c,则a⊥c | ||
| C. | 同位角相等 | D. | 在同一平面内,如果a∥b,b∥c,则a∥c |
8.“東星時代广場”六个字中,是轴对称图形的是( )
| A. | 東 | B. | 星 | C. | 時 | D. | 場 |
 如图,在△ABC中,D、E分别是AC、AB边上的点,若要△ADE与△ABC相似,则需要添加的一个条件是∠ADE=∠B.
如图,在△ABC中,D、E分别是AC、AB边上的点,若要△ADE与△ABC相似,则需要添加的一个条件是∠ADE=∠B.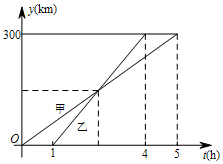 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距50千米时,$t=\frac{5}{4}$或$\frac{15}{4}$.以上结论正确的是①②.
甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距50千米时,$t=\frac{5}{4}$或$\frac{15}{4}$.以上结论正确的是①②.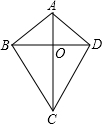 如图所示,AC、BD相交于点O,△ABO≌△ADO,下列结论正确的个数是( )
如图所示,AC、BD相交于点O,△ABO≌△ADO,下列结论正确的个数是( )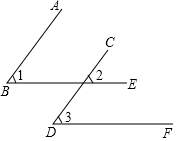 如图所示,已知AB∥CD,∠1=∠3,BE与DF平行吗?请说明理由.
如图所示,已知AB∥CD,∠1=∠3,BE与DF平行吗?请说明理由.