Question

15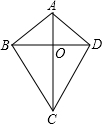．如图所示，AC、BD相交于点O，△ABO≌△ADO，下列结论正确的个数是（　　）
①AC⊥BD
②CB=CD
③△ABC≌△ADC
④AC平分∠BAD．

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 根据全等三角形的性质得出∠AOB=∠AOD=90°，OB=OD，AB=AD，再根据全等三角形的判定定理得出△ABC≌△ADC，进而得出其它结论．

解答 解：∵△ABO≌△ADO，
∴∠AOB=∠AOD=90°，OB=OD，AB=AD，
∴AC⊥BD，故①正确；
∵四边形ABCD的对角线AC、BD相交于点O，OB=OD，AC⊥BD，
∴BC=DC，②正确；
在△ABC和△ADC中，$\left\{\begin{array}{l}{AB=AD}\\{BC=DC}\\{AC=AC}\end{array}\right.$，
∴△ABC≌△ADC（SSS），故③正确；
∵△ABC≌△ADC，
∴∠BAC=∠DAC，
∴AC平分∠BAD，④正确；
正确结论有4个，
故选：D．

点评 本题考查了全等三角形的判定和性质、等腰三角形的性质，掌握全等三角形的判定方法是解题的关键．