题目内容
已知（m-1）2+|n+2|=0，那么（m+n）2014=（ ）
| A、-1 | B、1 |
| C、-2014 | D、2014 |
考点：非负数的性质：偶次方,非负数的性质：绝对值
专题：
分析：根据非负数的性质，可求出m、n的值，然后将代数式化简再代值计算．
解答：解：∵（m-1）2+|n+2|=0，
∴m-1=0，n+2=0
∴m=1，n=-2；
原式（m+n）2014=（1-2）2014
=1．
故选B．
∴m-1=0，n+2=0
∴m=1，n=-2；
原式（m+n）2014=（1-2）2014
=1．
故选B．
点评：本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
相关题目
某品牌儿童玩具原价100元，连续两次降价x%后售价为81元，下面所列方程中正确的是（ ）
| A、100（1+x%）2=81 |
| B、100（1+2x%）=81 |
| C、81（1-x%）2=100 |
| D、100（1-x%）2=81 |
如图所示，一架长为2.5米的梯子，斜靠在竖直的墙上，这时梯子的底端距离底0.7米，求梯子顶端离地多少米？如果梯子顶端沿墙下滑0.4m，那么梯子底端将向左滑动多少m？下列各数：-3.8，+5，0，-
，-（8），
，-4，-|-1|，其中属于负数的个数为（ ）
| 1 |
| 2 |
| 3 |
| 5 |
| A、3 | B、4 | C、5 | D、6 |
两个五次多项式相加，所得结果的次数是（ ）
| A、5 | B、10 |
| C、不大于5 | D、不小于5 |
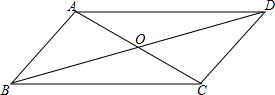已知?ABCD的周长为68cm，对角线交于点O，△ABO与△ADO的周长和等于80cm，两对角线的长度之比是2：3，求两条对角线的长度．
如图，△ABC内接于⊙O，且AB=BC=AC，M是