题目内容
15.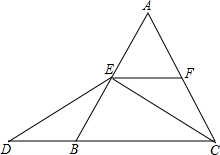 如图,在边长为2的等边△ABC中,E为AB的中点,EF∥BC,交AC于点F,点D为CB延长线上一点,且DE=EC.
如图,在边长为2的等边△ABC中,E为AB的中点,EF∥BC,交AC于点F,点D为CB延长线上一点,且DE=EC.(1)求四边形EFCB的周长;
(2)猜想线段AE与DB的大小关系,并说明你的理由.
分析 (1)首先根据E为AB的中点,EF∥BC,可得EF是△ABC的中位线,所以点F为AC的中点;然后求出EF的长度,再加上FC、CB、BE的长度,求出四边形EFCB的周长是多少即可;
(2)猜想线段AE=DB,首先根据等边三角形的性质以及中位线的性质,判断出∠ECF=∠FEC,∠FEC=∠ECB,所以∠ECB=∠ECF=30°,再根据DE=EC,可得∠D=30°,然后判断出∠DEB=30°,可得BE=DB,再根据AE=BE,判断出AE=DB即可.
解答 (1)解:∵E为AB的中点,EF∥BC,
∴EF是△ABC的中位线,
∴EF=$\frac{1}{2}BC=\frac{1}{2}×2=1$;
∴四边形EFCB的周长是:
EF+FC+CB+BE=1+2÷2+2+2÷2=5.
答:四边形EFCB的周长是5.
(2)猜想线段AE=DB,
证明:∵EF=CF,
∴∠ECF=∠FEC,∠FEC=∠ECB,
∴∠ECB=∠ECF=60÷2=30°;
∵DE=EC,
∴∠D=30°,
∴∠DEB=60-30=30°,∠D=30°,
∴∠DEB=∠D,
∴BE=DB,AE=BE,
∴AE=DB.
点评 (1)此题主要考查了等边三角形的性质,以及中位线的判定和性质,要熟练掌握;
(2)此题还考查了图形的周长的含义和求法,要熟练掌握.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
3.下列方程组是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{2x+3y=4}\\{2x+3=4(z+1)}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{10}{x}+3y=17}\\{8x-3y=1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{m}{2}=1}\\{2m+n=16}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x+2y}{z}=1}\\{\frac{2x-y}{3}=1}\end{array}\right.$ |
5.抛物线y=ax2+bx+c上部分点的横坐标x、纵坐标y的对应值如下表:
从上表可知,下列说法中正确的有(填写序号)( )
①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最值为6;③抛物线的对称轴是x=$\frac{1}{2}$;④在对称轴左侧,y随x的增大而增大.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最值为6;③抛物线的对称轴是x=$\frac{1}{2}$;④在对称轴左侧,y随x的增大而增大.
| A. | ①④ | B. | ②③ | C. | ①③④ | D. | ③④ |
 如图,在?ABCD中,E为AD的中点,AC与BE相交于点F,△EFC的面积为1cm2,求?ABCD的面积.
如图,在?ABCD中,E为AD的中点,AC与BE相交于点F,△EFC的面积为1cm2,求?ABCD的面积.