题目内容
20.用公式法解下列方程(1)x2+x-6=0;
(2)x2-$\sqrt{3}$x-$\frac{1}{4}$=0;
(3)3x2-6x-2=0;
(4)4x2-6x=0;
(5)x2+4x+8=4x+11;
(6)x(2x-4)=5-8x.
分析 各方程整理为一般形式,找出a,b,c的值,计算出根的判别式大于0,代入求根公式即可求出解.
解答 解:(1)a=1,b=1,c=-6,
∵△=1+24=25,
∴x=$\frac{-1±5}{2}$
解得:x1=2,x2=-3;
(2)a=1,b=-$\sqrt{3}$,c=-$\frac{1}{4}$,
∵△=3+1=4,
∴x=$\frac{\sqrt{3}±2}{2}$,
解得:x1=$\frac{\sqrt{3}}{2}$+1,x2=$\frac{\sqrt{3}}{2}$-1;
(3)a=3,b=-6,c=-2,
∵△=36+24=60,
∴x=$\frac{6±2\sqrt{15}}{6}$
解得:x1=1+$\frac{\sqrt{15}}{3}$,x2=1-$\frac{\sqrt{15}}{3}$;
(4)a=4,b=-6,
∵△=36,
∴x=$\frac{6±6}{8}$
解得:x1=$\frac{3}{2}$,x2=0;
(5)方程整理得:x2-3=0,
a=1,b=0,c=-3,
∵△=12,
∴x=±$\frac{2\sqrt{3}}{2}$,
解得:x1=$\sqrt{3}$,x2=-$\sqrt{3}$;
(6)整理得:2x2+4x-5=0,
a=2,b=4,c=-5,
∵△=16+40=56,
∴x=$\frac{-4±2\sqrt{14}}{4}$,
解得:x1=-1+$\frac{\sqrt{14}}{2}$,x2=-1-$\frac{\sqrt{14}}{2}$.
点评 此题考查了解一元二次方程-公式法,熟练掌握求根公式是解本题的关键.

练习册系列答案
相关题目
10.下列关于x的方程中,一定是一元二次方程的为( )
| A. | ax2+bx+c=0 | B. | x2=x(x+3) | C. | x2+3x-5=0 | D. | x2-y=0 |
15. 把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能( )
把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能( )
 把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能( )
把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能( )| A. | $\left\{\begin{array}{l}{x>4}\\{x≤-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x<4}\\{x≥-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x>4}\\{x>-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x≤4}\\{x>-1}\end{array}\right.$ |
9.若△ABC的周长是12cm,则△ABC三条中位线围成的三角形的周长为( )
| A. | 24cm | B. | 6cm | C. | 4cm | D. | 3cm |
 如图,C是线段AB的黄金分割点,BC>AC,D,E分别是AC,BC的中点.
如图,C是线段AB的黄金分割点,BC>AC,D,E分别是AC,BC的中点.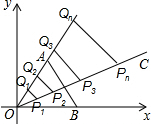 如图,在直角坐标系xOy中,点A在第一象限,点B在x轴的正半轴上,△AOB为正三角形,射线OC⊥AB,在OC上依次截取点P1,P2,P3,…,Pn,使OP1=1,P1P2=3,P2P3=5,…,Pn-1Pn=2n-1(n为正整数),分别过点P1,P2,P3,…,Pn向射线OA作垂线段,垂足分别为点Q1,Q2,Q3,…,Qn,则点Qn的坐标为($\frac{\sqrt{3}}{4}$n2,$\frac{3}{4}$n2).
如图,在直角坐标系xOy中,点A在第一象限,点B在x轴的正半轴上,△AOB为正三角形,射线OC⊥AB,在OC上依次截取点P1,P2,P3,…,Pn,使OP1=1,P1P2=3,P2P3=5,…,Pn-1Pn=2n-1(n为正整数),分别过点P1,P2,P3,…,Pn向射线OA作垂线段,垂足分别为点Q1,Q2,Q3,…,Qn,则点Qn的坐标为($\frac{\sqrt{3}}{4}$n2,$\frac{3}{4}$n2). 如图,点P到直线l的距离是1.8cm.(填入具体数值)
如图,点P到直线l的距离是1.8cm.(填入具体数值)