题目内容
12.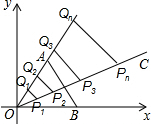 如图,在直角坐标系xOy中,点A在第一象限,点B在x轴的正半轴上,△AOB为正三角形,射线OC⊥AB,在OC上依次截取点P1,P2,P3,…,Pn,使OP1=1,P1P2=3,P2P3=5,…,Pn-1Pn=2n-1(n为正整数),分别过点P1,P2,P3,…,Pn向射线OA作垂线段,垂足分别为点Q1,Q2,Q3,…,Qn,则点Qn的坐标为($\frac{\sqrt{3}}{4}$n2,$\frac{3}{4}$n2).
如图,在直角坐标系xOy中,点A在第一象限,点B在x轴的正半轴上,△AOB为正三角形,射线OC⊥AB,在OC上依次截取点P1,P2,P3,…,Pn,使OP1=1,P1P2=3,P2P3=5,…,Pn-1Pn=2n-1(n为正整数),分别过点P1,P2,P3,…,Pn向射线OA作垂线段,垂足分别为点Q1,Q2,Q3,…,Qn,则点Qn的坐标为($\frac{\sqrt{3}}{4}$n2,$\frac{3}{4}$n2).
分析 利用特殊直角三角形求出OPn的值,再利用∠AOB=60°即可求出点Qn的坐标.
解答 解:∵△AOB为正三角形,射线OC⊥AB,
∴∠AOC=30°,
又∵Pn-1Pn=2n-1,PnQn⊥OA,
∴OQn=$\frac{\sqrt{3}}{2}$(OP1+P1P2+P2P3+…+Pn-1Pn)=$\frac{\sqrt{3}}{2}$(1+3+5+…+2n-1)=$\frac{\sqrt{3}}{2}$n2,
∴Qn的坐标为($\frac{\sqrt{3}}{2}$n2•cos60°,$\frac{\sqrt{3}}{2}$n2•sin60°),
∴Qn的坐标为($\frac{\sqrt{3}}{4}$n2,$\frac{3}{4}$n2).
故答案为:($\frac{\sqrt{3}}{4}$n2,$\frac{3}{4}$n2).
点评 本题主要考查了坐标与图形性质,解题的关键是正确的求出OQn的值.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
17.把直角三角形的两直角边同时扩大到原来的3倍,则其斜边扩大到原来的( )
| A. | 3倍 | B. | 6倍 | C. | 9倍 | D. | 18倍 |
4.已知(m-n)2=8,(m+n)2=2,则m2-n2=( )
| A. | 10 | B. | 6 | C. | ±4 | D. | 3 |
1.“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”设鸡为x只,兔为y只,则所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}x+y=35\\ x+2y=94\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=35\\ 4x+2y=94\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x+y=35\\ 2x+4y=94\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=35\\ 2x+2y=94\end{array}\right.$ |