题目内容
13.如图1,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.(1)求证:OE=OF;
(2)如图2,若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
(3)如图3,若点E在CA的延长线上,AM⊥BE于点M,交BD的延长线于点F,请你将图形补充完整,其他条件不变,则结论“OE=OF”还成立吗?
(提醒:先画图再回答、不需要说明理由;只回答、不画图不得分)

分析 (1)根据正方形的性质对角线垂直且平分,得到OB=OA,又因为AM⊥BE,所以∠MEA+∠MAE=90°=∠AFO+∠MAE,从而求证出Rt△BOE≌Rt△AOF,得到OE=OF.
(2)根据第一步得到的结果以及正方形的性质得到OB=OA,再根据已知条件求证出Rt△BOE≌Rt△AOF,得到OE=OF.
(3)如图3,同理可得OE=OF.
解答 (1)证明:∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO.
∴△BOE≌△AOF.
∴OE=OF.
(2)解:OE=OF成立.
证明:∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠F+∠MBF=90°,
∵∠E+∠OBE=90°,
又∵∠MBF=∠OBE,
∴∠F=∠E.
∴△BOE≌△AOF.
∴OE=OF.
(3)解:OE=OF成立.
证明:∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠F+∠MAM=90°,
∵∠F+∠OAF=90°,
又∵∠MAM=∠OAF,
∴∠F=∠E.
∴△BOE≌△AOF.
∴OE=OF.
点评 本题是四边形的综合题,考查了正方形的性质、三角形全等的性质和判定,并运用了类比的思想,三个问题都是证明△BOE≌△AOF解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.以下调查中,适宜全面调查的是( )
| A. | 调查春节联欢晚会的收视率 | |
| B. | 选出某校短跑最快的学生参加全区比赛 | |
| C. | 检测某批次火柴的质量 | |
| D. | 鞋厂检测生产的鞋底能承受的弯折次数 |
1.如图所示是某年11月的日历表:
请回答下列问题:
(1)若一竖列的三个数的和为42,请求出这三天的号数分别是多少?
(2)若在2×2的矩形方块中的四个数的和为80,请求出这四天的号数;
(3)如果是3×3的矩形方块中,九个数的和是171,你能求出这九个数中最小的数吗?若能,请求出这个数;若不能,请说明理由;你能发现这九个数的和与最中间的数有什么关系吗?请说明理由.
| 星期六 | 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
(1)若一竖列的三个数的和为42,请求出这三天的号数分别是多少?
(2)若在2×2的矩形方块中的四个数的和为80,请求出这四天的号数;
(3)如果是3×3的矩形方块中,九个数的和是171,你能求出这九个数中最小的数吗?若能,请求出这个数;若不能,请说明理由;你能发现这九个数的和与最中间的数有什么关系吗?请说明理由.
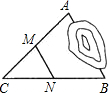 如图,A、B两点分布在水池的两边,一学生在AB外选取了一点C,连接AC和BC,并分别找出各自中点M、N,若测得MN=20m,则A、B两点的距离为( )
如图,A、B两点分布在水池的两边,一学生在AB外选取了一点C,连接AC和BC,并分别找出各自中点M、N,若测得MN=20m,则A、B两点的距离为( ) 如图,已知直线a∥b,点A在直线a上,点B、C在直线b上,点P在线段AB上,∠1=70°,∠2=100°,那么∠PCB=30度.
如图,已知直线a∥b,点A在直线a上,点B、C在直线b上,点P在线段AB上,∠1=70°,∠2=100°,那么∠PCB=30度.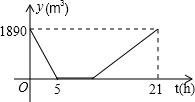 某游泳池内现存水1890(m3),已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水--清洗--灌水”的过程,其中游泳池内剩余的水量y(m3)与换水时间t(h)之间的函数关系如图所示.根据图象解答下列问题:
某游泳池内现存水1890(m3),已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水--清洗--灌水”的过程,其中游泳池内剩余的水量y(m3)与换水时间t(h)之间的函数关系如图所示.根据图象解答下列问题: 若想检验一块儿破损的木板的两条直的边缘AB,CD是否平行,你的办法是画一条直线截线段AB与CD,测量一对同位角,如果相等,则AB∥CD,反之,则不平行.(工具不限,可结合图形进行说明,只要能说清思路即可)
若想检验一块儿破损的木板的两条直的边缘AB,CD是否平行,你的办法是画一条直线截线段AB与CD,测量一对同位角,如果相等,则AB∥CD,反之,则不平行.(工具不限,可结合图形进行说明,只要能说清思路即可)