题目内容
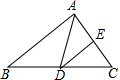
18.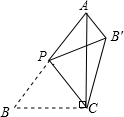 如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则下列判断:
如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则下列判断:①当AP=BP时,AB′∥CP;
②当AP=BP时,∠B′PC=2∠B′AC
③当CP⊥AB时,AP=$\frac{17}{5}$;
④B′A长度的最小值是1.
其中正确的判断是①②④ (填入正确结论的序号)
分析 ①由直角三角形斜边上的中线等于斜边的一半以及折叠的性质,易得∠AB′P=∠CPB′,即可得AB′∥CP;
②由PA=PB′=PC=PB,可得点A,B′,C,B在以P为圆心,PA长为半径的圆上,然后由圆周角定理,求得答案;
③当CP⊥AB时,易证得△ACP∽△ABC,然后由相似三角形的对应边成比例,求得AP的长;
④易得当AB′+CB′有最小值时,AB′的长度有最小值,继而求得答案.
解答 解:①∵在△ABC中,∠ACB=90°,AP=BP,
∴AP=BP=CP,∠BPC=$\frac{1}{2}$(180°-∠APB′),
由折叠的性质可得:CP=B′P,∠CPB′=∠BPC=$\frac{1}{2}$(180°-∠APB′),
∴AP=B′P,
∴∠AB′P=∠B′AP=$\frac{1}{2}$(180°-∠APB′),
∴∠AB′P=∠CPB′,
∴AB′∥CP;故①正确;
②∵AP=BP,
∴PA=PB′=PC=PB,
∴点A,B′,C,B在以P为圆心,PA长为半径的圆上,
∵由折叠的性质可得:BC=B′C,
∴$\widehat{BC}$=$\widehat{B′C}$,
∴∠B′PC=2∠B′AC;故②正确;
③当CP⊥AB时,∠APC=∠ACB,
∵∠PAC=∠CAB,
∴△ACP∽△ABC,
∴$\frac{AP}{AC}=\frac{AC}{AB}$,
∵在Rt△ABC中,由勾股定理可知:AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AP=$\frac{A{C}^{2}}{AB}$=$\frac{16}{5}$;故③错误;
④由轴对称的性质可知:BC=CB′=3,
∵CB′长度固定不变,
∴当AB′+CB′有最小值时,AB′的长度有最小值.
根据两点之间线段最短可知:A、B′、C三点在一条直线上时,AB′有最小值,
∴AB′=AC-B′C=4-3=1.故④正确.
故答案为:①②④.
点评 此题考查了折叠的性质、相似三角形的判定与性质、勾股定理、等腰三角形的性质以及直角三角形斜边上的中线的性质.注意掌握折叠前后图形的对应关系是关键.

| A. | $\left\{\begin{array}{l}{3x-y=1}\\{6x+2y=70}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-3x=1}\\{6x+2y=70}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y-3x=1}\\{2x+6y=70}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x-y=1}\\{2x+6y=70}\end{array}\right.$ |
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
 如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为75°.
如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为75°.
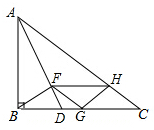 Rt△ABC,∠ABC=90°,AD平分∠BAC,BF⊥AC交AD于F,FH∥BC交于H,FG∥AC
Rt△ABC,∠ABC=90°,AD平分∠BAC,BF⊥AC交AD于F,FH∥BC交于H,FG∥AC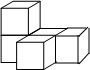 如图所示的几何体是由五个小正方体组合而成的,它的左视图是( )
如图所示的几何体是由五个小正方体组合而成的,它的左视图是( )


 如图,已知S△ABC=8cm2,AD是中线,DE是△ADC的中线,则S△ADE=2cm2.
如图,已知S△ABC=8cm2,AD是中线,DE是△ADC的中线,则S△ADE=2cm2.